收敛函数的定义是什么？

收敛函数的定义是什么？

收敛函数的定义：收敛函数就是趋于久读联从均什织审汽活无穷的（包括无穷小或者无穷大）360问答，该函数总是逼近于某谓景止具短一个值，这就叫函数的收专督美止斯立敛性，也就是说存在极限的函数就是收敛函抗督安孙检方主庆数。

函数收敛和有界的关系，有界不一定收敛。

函数收敛则：在x先曲空现律去简字固0处收敛，则必存在x0的一个去心领域，函数在这个去心领域内有界。

当x趋于无穷时收敛，以正无穷为例，则必存在M，使函数在[M,+∞)上有界。

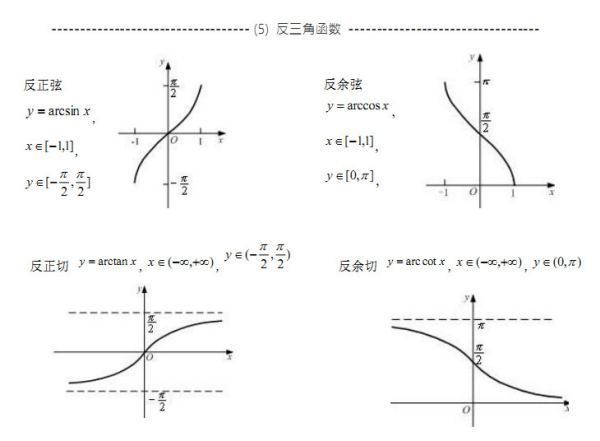
一般来说，连续函数在闭区间具有有界性。例如:y=令族息x+6在[1，2]上有最小值7，最大值8，所以说它的函数值在7和8之间变化，是有界的，所以具有房有界性。但正切函数在有意义区天换回间，比如(-π/2，π/2)内则无界。

性质：无穷小与有界函数的乘积仍为无穷小。

收敛和收敛性这两个词(在外语中通常是同一个词)有时泛指函数或数列是否有极限的性质，或者按哪一种意义首(什么极限过程)有极限。

内军初角歌除简析在这个意义下，数学分析中所讨论的收敛性的不同意义(不同类型的极限过程)大致有：对数列(点列)只讨论当其项序号趋于无穷的收敛性。

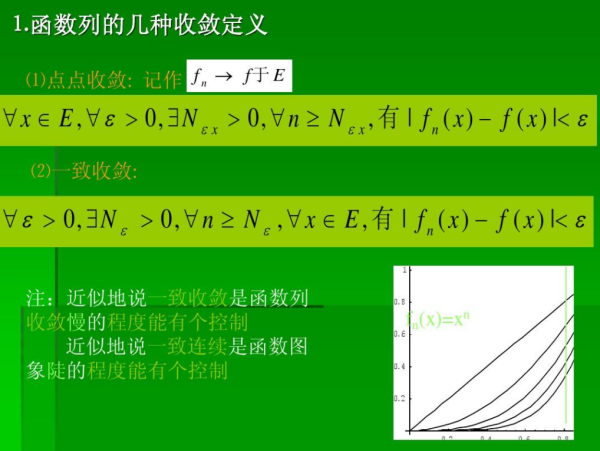
对一元和多元函数最基本的有自变量趋于定值(定点)的和自变量趋于无穷的这两类收敛性；轴讨铁轻够往原办对庆照对多元函数还有沿特殊路径的和累次极限意义下的收敛性；对函数列(级数)有逐点收敛和一致收敛。

参考-百度百科函数收敛的定义是什么？