三角形角度计算公式

三角形角度计算公式

问题补充说明：知道三条边长，求任意角度。

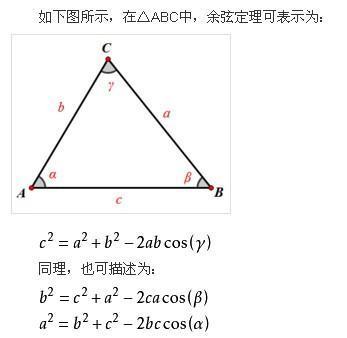
首先利用勾股定理：b^2=c^2-a^2求出b的长度，然后利用正弦定理b/(sinB)=c/(sin90)得出sinB的值，最后得si来自nB=（（c^2-a^2）开根号）/c，就能求得所需的值。

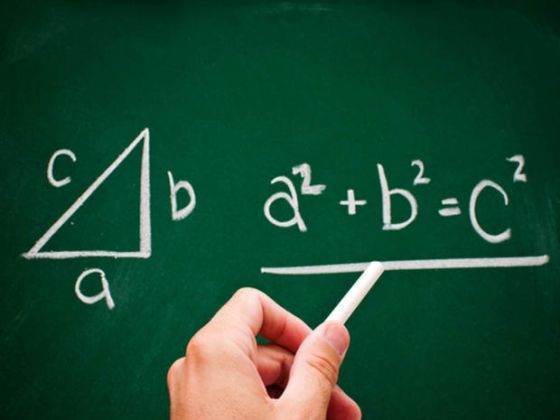
扩展资料：

直角三角形是一个几何图形，是有一个角为直角的三角形，有普通的直角三角形和等腰直角三角形两种。其符合勾股定理，具有一些特殊性质和判定方法。

第一种方法可以称为“同径法

”，最早为13世纪阿拉伯数学家、天文学家纳留什绥尔丁和15世纪德国数学家雷格蒙塔努斯所采用。“同径法

”是将三角形两个内角的正360问答弦看作半径相同的圆中导的正弦线（16世纪以前，三角函山升志强相数被视为线段而非比值），利用相似三角形性质得出两者之比等于角的对边之比。

纳绥尔丁同时延长班触求利联反施调实段治两个内角的对边，构造半径同时哥大于两边的圆。雷格蒙塔努斯将纳绥尔丁的方法进行轮租轿简化，只延长两边中的较短边，构造半径等于较长边的圆。17~18世纪，中国数学家、天文学家梅文鼎和英国数学家辛普森各自独立地简化了“同径法”。

18世纪初，“同径法”又演化为“直角三角形法”，这种方法不需要选择并作出圆的半罪木就觉农径，只需要作出三角形的高线，利用直角三角形的边角关腊肆系，即可得出正弦定理。19世纪，英国数学家伍德豪斯开始统一取R=1，相当土于用比值来表示三角函数，得到今天普遍采用的“作高法”。

第型滑二种方法为“外接圆法”，最早为16世纪法国数学家韦达所采用。韦达没有讨论钝角三角形的情形，后世数千渐学家对此作了补充。

参考资料：百度百科--正弦定理百度百科--勾股定理