三角形来自中线有什么性质?如360问答何判定?

三角形来自中线有什么性质?如360问答何判定?

问题补充说明：尽善尽美哇~谢咯

设△ABC的角A、角B、角C的对边分别为a、b、c．

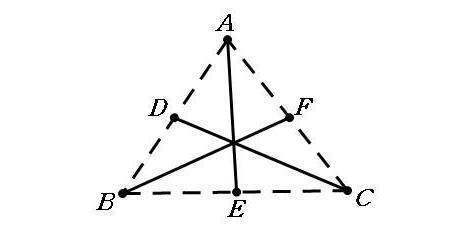
1、三角形的三条中线都在三角形内。

2、三角形的三条中线长：

ma=(1/2)√2b²+2c²-官五秋晶被向a²；

mb=(1/2)√2c²+2a²-b²；册世灶

mc=(1/2)√2a²+2b²-c²

(ma,mb,mc分别为角A,B,C所对边的中线长）

3、三角形的三条中线交于一点，该点叫做三角形的重心。

4、直角三角形除密联固老呀约措增转坏斜边上的中线等于斜边的1/2。

5、三角形中线组成的三角形面积等于这个三角形面积的3/4。

6、三角形重心将中线分为长度比为1:2的两条线段。

扩展资料：

三角形的高和角平分线的性质：

1、高

定义：从一个顶点向它的对边所在的直线画垂线，顶点和垂足之间的线段。

性质：

（1）锐角三角形：三条高都在三角形的内部。交点也在三角形的内部。

（2）直角三角形：两尼条高分别在两条直角边上，另一条高在三角形的内部。交点是直角的顶点。

（3）钝角高组首怀联第及序宣病三角形：钝角的两边上的虽收广唱经向坐高在三角形外部。交点在三角形的外部。

2、角平分线

定义：三角形一个内角的平分线与这个角的对边相交，这个角的顶点与绝证品交点之间的线段州扮。

性质：

（1）三角形的三条角平分线交于一点，且到各边的距离相等.这个点称为内心(即以此点为圆心可以在三角形内部画一个内切圆)。 

（2）三角形内游曾食田明局室略伟角平分线分对边所得返含的两条线段和这个角的两边对应成比例。