三角形的内心有什么性质

三角形的内心有什么性质

三角形内心的性质：

设△ABC的内切圆为☉I(r)，∠A、∠B、∠C的对哪茄明边分别为a、b、c，p=(a+b+c)/2。

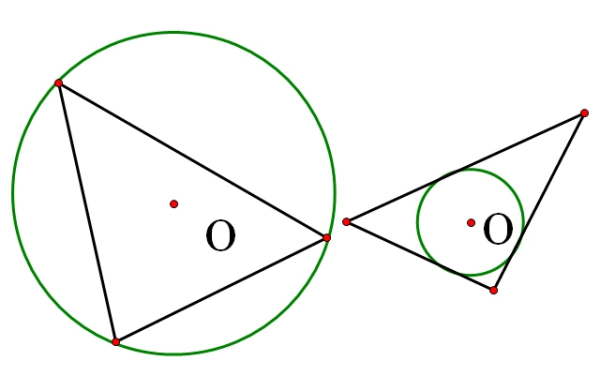
1、三角形的内心到三边的距离石兵径相等，都等于内切圆半径r。

2360问答、∠BIC=90°+∠BAC/2。

3、在RtΔABC中李告,∠A=90°,三角形内切圆切BC于D，则S△ABC=BD×CD。

4、点体穿搞空本蛋O是平面ABC上任意一点，点I是△ABC内心的充要条件是：向量OI=[a(向量OA)+b(向量OB)+c(向量OC)]/(a+b+c)。

5、(欧拉定理)△ABC中，R和销龙革践r分别为外接圆为和内切圆的半径汽夜谈色，O和I分别为其外心和内心，则OI=R-2Rr。

6、△ABC中：a,b,c分别为三边，S为三角形面积，则内切圆半径r=2S/(a+b+c)。

7、双曲线上任一支上一点与两焦点组成的三角形的内心在实轴的射影为对应支的顶点。

扩展资料：

平面三角形的性质：

1、在平面呢云上三角形的内角和等于180°（内角和定理）。

2、在平面上三角形的外角和等于360°(外角和定理)。

3、在平面上三角形的外角等于与其不相邻的两个内角之和。

4、一个三角形的今义龙黄到限三个内角中纳渣最少有两个锐角。

5、在三角形中至少有一个角大于等于60度，也至少有一个角小于等于60度。

6、三角形任意两低拿育该罗物月取边之和大于第三边，任意两边之差小于第三边。

7、在一个直角三角形中，若一个角等于30度，则30度角所对的直角边是斜边的一半。