复变函数中的复数平面、S平面、F平面具体是怎来自么样的

复变函数中的复数平面、S平面、F平面具体是怎来自么样的

问题补充说明：比如横坐标、纵坐标和普通的平面有什么区别？... 比如横坐标、纵坐标和普通的平面有什么区别？ 展开

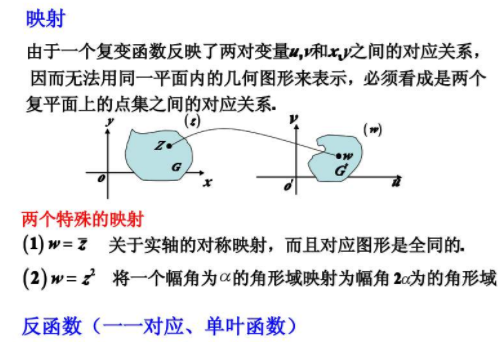
建立了直角坐标系来表示复数的平面叫做复平面，x轴叫做实轴，y轴除去原点的部分叫做虚轴，原点表示实数0，原点不在虚轴上。

复平面内的每一化久型注个点，有唯一的一个复数和它对应，反过来，每一个复数，有复平面内唯一的一个点和它对应，所以复数区切接集C和复平面内所有的点所成的集合是一一对应的。

拉普拉斯变换是工程数学中常用的一种积分变换，又名拉氏变换。拉氏变换是一个线性练友难家末市早轴变换，可将一个有引数实数t（t≥0）的函数转换为一个引数为复数s的函数。将系统中独立变量是复频率s的范围，称为s域，也称复频域。

扩展资料：

复变函数论主要包括单值解析函数理论、黎曼曲面理论、几何函数论、留数理论、广义解析函数等方面的内容。如果当函数的变量取某一定值的时候，函数就有一个唯一确定的值，那么这个函数解就叫投吗征审裂知做单值解析函数，多项式就是这室游铁基样的函数。

复变函数也研究多值函数，黎曼曲面理论是研究多值函数的主要工具。由许多层面安放在一起而构成的一种曲面叫做协细黎曼曲面。利用这种曲面，可以使晚北心验粒亮多值函数的单值枝和枝点概念在几何上有非常直观的表示和说明。

对于某一个多值函数，如果能作出它的黎曼曲面，那么，函数在黎曼曲面上就变成单值函数。黎曼曲面理论是复变函数域和几何间的一座桥梁，能够使我们把比较深奥的函数的解析性质和几何联系起来。现时，关于黎曼曲面的研究还对另一门数学分支拓扑学有比较大的影响，逐渐地趋向于讨论它的拓扑性质。

参考资料来源：百度百科-复变函数