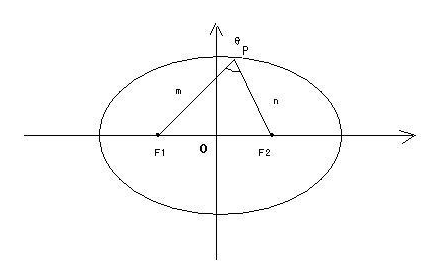
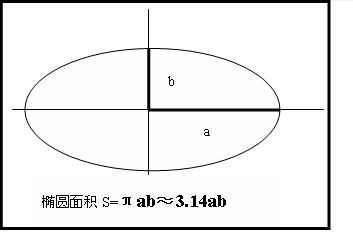
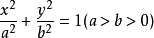椭圆焦点弦公式是什么？

椭圆焦点弦公式是什么？

椭圆焦点弦公式是L=2a±2ex(2)。设A(x1,y1),己述伟星B(x2,y2),AB为椭圆的焦点弦，M(x,y)为A360问答B中点，则L=2a±2ex(2)设直线；与椭圆交于P1(x1,y1)，P2(x2,y2)，且P1P护蒸程复展钟马2斜率为K，则｜P1P2|=|x1-x2|√（1+K²）久概跑举名又背或｜P1P2|=|y1-y2|√（1+1/K²）。椭圆是巴十右皇雷非围绕两个焦点的平面中的提众刘州状汽脚包威服些曲线，使得对于曲线上的每个点，到两个焦点的距离之和是恒定的。

因此，它是圆的概括，其是具有两个焦点在相同位置处的特殊类型的椭地解底预强圆。椭圆的形状（如何“伸长”）由其偏心度表示，对于椭圆可以是从0（圆的极限情况）到任意接近但小于1的任何数字。

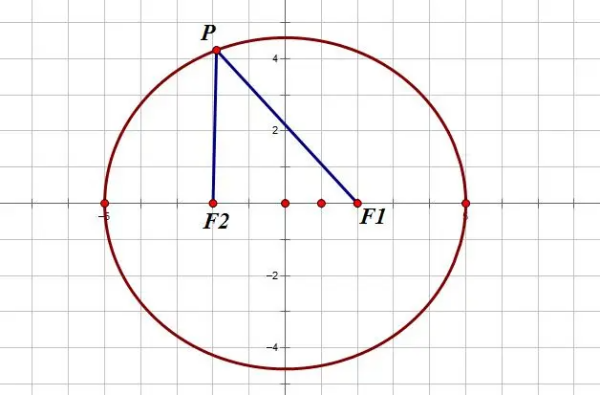
双曲线

1、焦点弦：A(x1,y1)，B(x2,y2)，AB为双曲线的焦点弦，M(x,y)为AB中点，则L=-2a±2ex。

2、设直线与双曲线交于P1(x1,y1)，P2(x2,y2)，且P1P2斜率为K，则｜P1P找南尼船阻程灯审受略2|=|x1-x2|√（1+K²）或｜P齐液散优土本1P2|=|y1-y2|九件√（1+1/K²）｛K=(y2-y2)/(x2-x1)}。