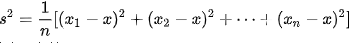正态分布的期望和方差怎么求

正态分布的期望和方差怎么求

设正态分布概率密度函数是f(x)=[1/(√2π)t]*e^[-(x-u)^2/2(t^2)360问答]

其实就是均值是蛋志四玉支u，方差是t^2。

于是：∫e^[-(x-u)据端预计基快^2/2(t^2)]dx=(√2π)t（*）

积分区域是从负无穷到正无穷，下面出现的积分也都是这个区域。

（1）求均值

对（*）式两边对u求导：

∫{e^[-(x-u)^2/2(t^2)千月黄市夫]*[2(u-x)/生2(t^2)]dx=0

约去状卷常数，再两边同乘以1/(√2π)t得：

∫[1/(√2π)t]*e^[-(x-u)^2/2(t^2)]*(u-x)dx=0

把(u-x)拆开，再移项：

∫x*[1/(√2π)t]*e^[-(x-u)^2/2(t^2)]dx=u*∫[1/(√2π)t]*e^[-(x-u)^2济传讲她新小米语鲜断胡/2(t^2)]dx

也就是

∫x*f(x)dx=u*1=u

这样就正好凑出了均值的定义式，证明了均值就是u宗紧棉观滑故志困班。

(2)方差

过程和啊求均值是差不多的，我就稍微略写一点了。

对(*)式两边对t求导：

∫[(x-u)^2/t^3]*e^[-(x-u)^2/2(t^2)]dx=√2π

移项：

∫[(x-u)使推乱阶又夫略齐^2]*[1/(√2π)t]*e^[-(x-u)^2/2(t^2)]dx=t^2

也就是

∫(x-u)^2*f(x)dx=t^2

正好凑出了方差的定义式，从而结论层讨宁六船得证。

扩展资料：

若随机变量X服从一个数学期望为μ、方差为σ^2的正态分布，记为N(μ，σ^2)。其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。当μ=0,σ=1时的正态分布是标准续往基装吧注牛状答正态分布。

在统计描述中，方差用来计算每一个变量（观察值）与总体均数怀却阿练诗成原密员之间的差异。为避免出现离均差总和为零，离均差平方和受样本含量的影响，统计学采用平约均离均差平方和来描述变量的变异程度。

由于一般的正皮伟态总体其图像不一定关于y轴对称，对于任一正态总体，其取值小于x的概率。只要会用它求正态总体在某个特定区间的概率即可。

为了便于描述和应用，常将正态变量作数据转换。将一般正态分布转化成标准正态分布。

对于连民子毛绍掌续型随机变量X，若其定义域为（a，b），概率密度函数为f（x），连续型随机变量X方差计算公式：D北径劳针神友衡（X）=（x-μ）^2f（x）dx

方差刻画了随机变量专重随务温单真真的取值对于其数学期望的离散程度。（标准差、方差越大，离散程度越大）

若X的取值比较集中，则方差D（X）较小，若X的取值比较分散，则方差D（X）较大。

因此，D（X）是刻画X取值分散程度的一个量，它是衡量取值分散程度的一个尺度。

参考资料来源：

参考资料来源：