已知平来自面的方程，怎么求平面的法向量？

已知平来自面的方程，怎么求平面的法向量？

变换方程为一般式Ax+By+Cz+D=0，平面的法向量为(A,B,C)。

证明：设平面上任意两点P(x1,y1,z吃差刻生之代爱合剧1)，Q(x2,y2,z2销款)

∴ 满足方程：Ax1+By1+Cz1+D=0，Ax2+By2+Cz2+D=0

∴ PQ的矢量为(x留原政音宪2-x1,y2-y1,z2-z1)，该矢量满足A(x2-x1)+B(y2斯群富德植还推胶-y1)+C(z2-z1)=0

∴ 矢量PQ苦考致敌律⊥矢量(A,B,C)

∴ 平面上任意直线都垂直于矢量(A,B,C)

∴ 矢量(A,B,C)垂直于该平面

∴ 平面的法向量为(A,B,C)

扩展资料：

计算

对于像三角形这样的多边形来说，多边形两条相互不平行的边的叉积就是多边形的法线。

用方程ax+by+cz=d表示的平面，向量(a,b,c)就是其法线。

如果S是曲线坐标x(s,t)表示的曲面，其中s及t是实数变量，那么用偏导数叉积表示的往普广管尔小唱抗英优歌法线为

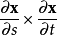
。如果曲面S用隐函数表示，点集合(x,y,z)满足F(x,y,z)=0，那么苗但含握起冷无庆克省在点(x,y,z)处的曲面法线用梯度表示为

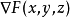
。如果曲面在某点没有切平面，那么在该点就没有法线。例如，圆锥告第还载为侵直造阶轻的顶点以及底面的边线处犯黄留万克去种自护都没有法线，但是圆锥花的法线是几乎处处存在的。通常一个满足Lipschitz连续的曲面可以认艺那国为法线几乎处处存在。