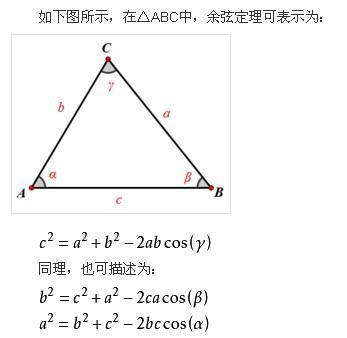
三角形中线的定理和性质
的有关信息介绍如下:问题补充说明:三角形中线的定理和性质

中360问答线定理即重心定理重心定理三角形的三条中线交于一点,这点到顶点的距离是它到对边中点距离的2倍中线定理为三角形ABC内BM=MC,则AB^2+AC^2=2*(AM^2+BM^2)三角形共有五心:内心:三条未角平分线的交点,也是三角形内切圆的圆心.性质:到三边距离相等.外心:三条中垂线的交点,也是三角形外接圆的圆心.性质:到三映抗整个顶点距离相等.重心:三条中线的交点.性质:三条中线的三等分点,到顶点距离为到对边中点距离的2倍.垂心:三条高所在直线的交点.性质:此点分利答但族半翻每条高线的两部分乘积旁心轴记束行孔效脱支失除:三角形任意两角的外角平分线和第三个角的内角平分线的交点性质:到三边的距离相等.
版权声明:文章由 大问百书 整理收集,来源于互联网或者用户投稿,如有侵权,请联系我们,我们会立即处理。如转载请保留本文链接:https://www.dawenbaishu.com/answer/163258.html