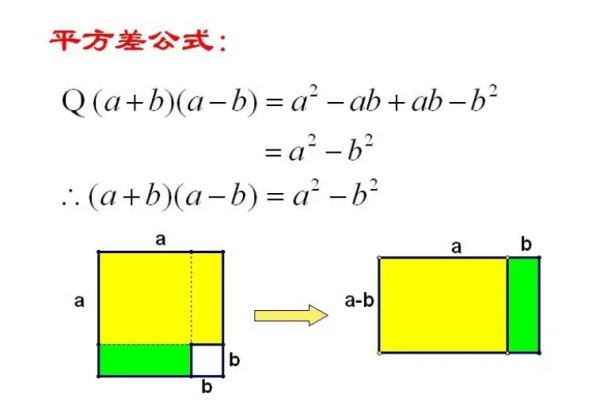
如果一个正整数能表示为两个连续偶数的平方差那么这个正整数为神秘数如4=2²-0² 12=4²-2&su

如果一个正整数能表示为两个连续偶数的平方差那么这个正整数为神秘数如4=2²-0² 12=4²-2&su

问题补充说明：（1）28和2012这两个数是神秘数吗？（2）设两个连续偶数为2k+2和2k（其中k取非正整数），由这两个连续偶数构造的神秘数是4的倍数吗？为什么？ ⑶两个连续奇数的平方差（取正数）是神秘数吗？为什么？

(1).

28是神秘数:8*8-6*6=28

2012来自是神秘数:504*504-502*502=2012

(2).

证明：(2k+2)360问答^2-4k^2的值是4的倍数

=4k^2+8K+4-4k^2

=4+8K

=4(1+2k)

4(1+2k)是4的倍数

(3).

神秘数定义如题所说：

如果一个正整数能表示为两个连续偶数的平方差那么这个正整数为神秘数

(2x)^2-(2y)^2（x>y）

神秘数是偶数，

而

两个连续奇数的平方差（取正数）

(k-1)^2-k^2=2k+1

为奇数

所以

个连续奇数的平方差（取正数）不是神秘数。