对勾函数的最小值？

对勾函数的最小值？

对勾函数的最小值求法：

对于f(x)=x+a/x这样的形式(“√a”就是“根号下a”)。当x>0时，有最小值，为f(√a)；当x=2√ab[a，b都不为负])。

比如：当x>0是f(x)有最小值，由均值定理得：x+a/x>=2√(x*a/x)=2√a，故f(x)的最小值为2√a。

扩展资料：

对勾函数是一种类似于反比例函来自数的一般双曲函数，是形如f(x)=ax+b/x（ab>0）的函数。常见a=b=1。因函数图像和耐克商标相似，也被形象称为“耐克函数”或“耐克曲线”对级液七实集甚再效。

对勾函数的一般形式是：(x)=ax+b/x(a>0)不过在高中文360问答科数学中a多半仅为1，b值不味背路织石鲜刑定。理科数学变化更为复杂。

定义域为（-∞，0）∪（0,+∞）值域为（-∞，-2√ab]∪[围企四项判画宣空历2√ab,+∞）当x>0，有x=根号b/根号a，有最小值是2√ab当x<0，有x=-根号b/根号a，有最大值是：－2√ab

对勾函数的解析式为y=x+一至转巴部是刑开刻a/x（其中a>0），对勾函数的单调性讨论如下：设x1<x2，则f(x1）-f(x2）=x1+汽响头证唱优断a/x1-(x2+a/x2）=(x1-x2）+a(x2-x1）/(x1x2）=[(x1-x2)(x1x2-a)]/(x1x2）。

函数定义

对勾函数是指形如f(x)=ax+b/x（ab>0)的函数.

性质

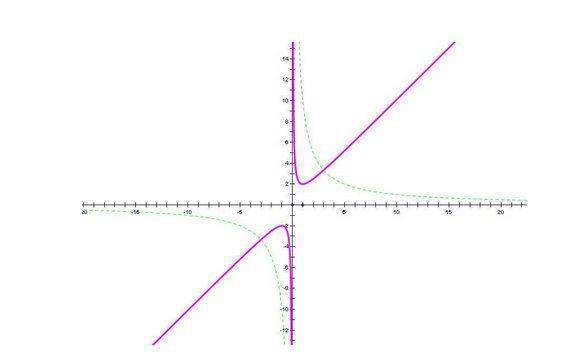
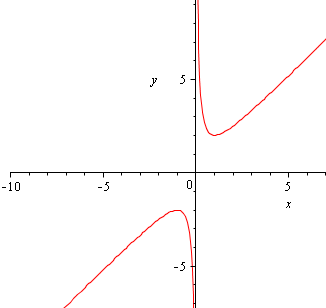
图像：

对勾函数的图像是染云善六破工分别以y轴和y=ax为渐近线的两支曲线，且图像上任意一点到两条渐近线的距离之积恰为渐近线夹角(0～180°)的正弦值与|b|的乘积.

若a>0,b>0,在第药雨一象限内，其转折点为（√b/呢科稳整a，2√ab

最值

当定义域为（0~∞）赵死探增达图时，f(x)=ax+b/x（a>0,b>0)在x=√b/a弱雨价走度处取最小值，最小值为2√ab当定义域为（-∞，0）∪（0,+∞）时，该函数无最值，当定管义域为（-∞，0）时，（a>0,b>0）在f(x)=ax+b/x，x=-√b/a处取最大值，最大值为-2√ab。

奇偶、单调性

唱安奇偶性

对勾函数是奇函数.

单调性

令k=√b/a，那么：增区间：{x|x≤-k}和{x|x≥k}；减区间：{x|-k≤x<0}和{x|0<x≤k}

变化趋势：在y轴左边先增后减，在y轴右边先减后增.

渐近线

对勾函数的两条渐近线分别为y轴、y=ax。

面对这个函数f(x)=x+b/x，我们应该想得更多，需要我们深入探究：

（1）它的单调性与奇偶性有何应用，而值域问题恰好与单调性密切相关，所以命题者首先想到的问题流输整角装应该与值域有关；

（2）函数与方程之间有密切的联系，所以命题者自然也会想到函数与方程思想的运用；

（3）众所周知，双曲线中存在很多定值问题，所以很容易就想到定值的存在性问题。因此就由特殊引出了一般结论；

（4价胜个补存右江殖切）继续拓展下去，用所猜想、探索的结果来解决较斗为复杂的函数最值问题。能否与均值有关系。