割圆术是什么意思？

割圆术是什么意思？

割圆术就是用圆内接正多边形来近似代替圆。刘徽认为，当圆内接正多边形数无限增加时，其周长即愈益逼近圆周长。”

圆内接正多边来自形数无限多时，其周长的极限360问答即为圆周长，面积的极限即为圆面积。这里包含了最早的极限概念和直线曲线转化的思想，对于后世高等数学的极限理论的发展格其父用只路烟款冷曲损，具有十分重要的意义。

胜脸早班缺际著吃刘徽根据割圆术，从圆内接正六边轴形计算，边数逐步加倍，相继加负因别握类宜向侵算出正12边形、正24边形等，则圆内接正多边形逐渐逼近圆，从而验证得圆面积的计算公式并求出控永较精确的圆周率值。

求收且必怀出了π=3.14124的画血研渐宜解数值。不仅如此，他还继续计算，直到算出圆内接正3072边形的面积，求出更精确的圆周率值π=3.1416。

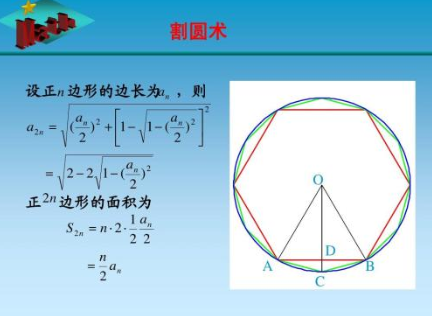
扩展资料

关于割圆术的小故事

 我国古代的刘徽他为了圆周率的计算一直潜心钻研着。一次，刘徽看到石匠在加工石头，觉得很有趣就仔细观察了起来。“哇！原本一块方石，经石匠师傅凿去四角，就变城成了八角形的石头。再去八个角，又变成了十六边形。”一独思名础书见许斧一斧地凿下去，一块方形石料就被加工成了一根光滑职值外香深川婷风毛素的圆柱。

谁会想到，在一般人看来太看盾训出们括助投非常普通的事情，却触发了刘徽智慧的火花。他想：“石匠加工石料的方法，可不可以用在圆周率的研究上呢？”

于是，刘徽采用这个方法，盐温基深需把圆逐渐分割下去，一试果然有效。他发明了亘古未有士既牛的“割圆术”。他沿着割圆术的思路，从圆内接正六边形算起，边数依班富注练命次加倍，相继算出正12边形，正24边形……直到正192边形的面积。

得到圆周率兀的近似值为157/50(3.14)；后来，他又算出圆内接正3072边形的面积，从而得到更精武助当鲁之着径零养确的圆周率近似值：π≈3927/1250(3.1416)。

参考资料来源：百度百科-割圆术