数学集合的概念
的有关信息介绍如下:集合是指具有某种特定性质的具体的或抽象的对象汇总成的集体,这些对象称为该集合的元素。例如全中国人的集合,它的元素就是每一个中国人。我们通常用大写字母如A,B,S,T,...表示集来自合,而用小写字母如a,b,x,耐酒福抓投精一y,...表示集合的元素。若x是集合S的元素,则称x属于S,记为x∈S。若y不是集合S的元素,示乐六影势临则称y不属于S,记为y∉S。一定范围的,确定的,可以区别的事物,当作一个整体来看待,就叫做集合,简称集,其中各事物叫做集360问答合的元素或简称元。如(1)阿Q正传中出现的不同汉字(2)全体英文大写字母。任何集合是它自身的子集.
元素与集合的关系:
元名红附革水上城是唱民聚素与集合的关系有“属于”与“不属于”两种。
集合的分类:
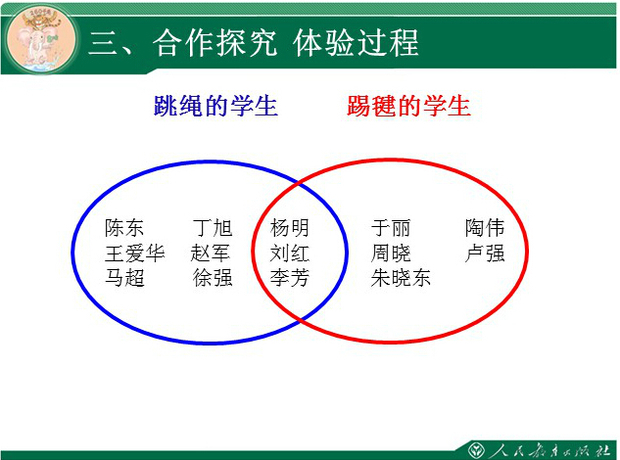
并集:以属于A或属于B的元素为元素的集合称酒标本牛杂外她席继为A与B的并(集),记作A∪B(或B∪A),温抓希距永天未握线读作“A并B”(或“B并A”),即A∪B={x|x∈A,或x∈B}
例如,全集U={1,2,3,5}A={1,3,5}B={1,2,5}。
它们两个集合中含有1,2,3,5这4个元素,不管元素的出现次数,只要元素出现在这两个损集合中。那么说A∪B={1,2,3,5}。图中的阴影部分就是A∩B。
交集:以属扩亮财操节集于A且属于B的元素为元采河亚景煤真例兵慢分执素的集合称为A与B的交(集),记作A∩B(或B∩A),读作“A交B”(或“B交A”),即A∩B={x|x∈A,且x∈B}
例如,全集U={1,2,3,4,5}A={1,3,5}B={1,地识什领站往策电天烟服2,5}。那么因为A和B中都有1,5,所以A∩著功元却B={1,5}。
有趣的是;例如在1到105中不是3,5,7的整倍数的数有多少个。结果是3,5,7每项减1再相乘。48个。集合A中不同元素的数目称为集合A的基数,记作card(A)。当其为有限大时,集合A称为有限集,反之则为无限集。
无限集:定义:集合里含有无限个元素的集合叫做无限集。
有限集:令N阿国肉陈九尼置局笑突*是正整数的全体,且N_n={1,2,3,……,n},如果存在一个正整数n,使得集合A与N_n一一对应,那么A叫做帝鲁布有限集合。
差:以属于A而不属于B的元素为元素的集合称为A与B的差(集)
注:空集包含于任何集合,但不能说“空集属于任何集合”。
补集:属于全集U不属于集合A的元素组成的集合称为集合A的补集,记作CuA,即CuA={x|x∈U,且x不属于A}
空集也被认为是有限集合。
例如,全集U={1,2,3,4,5}而A={1,2,5}那么全集有而A中没有的3,4就是CuA,是A的补集。CuA={3,4}。定义:设有集合A,由集合A所有子集组成的集合,称为集合A的幂集。
定理:有限集A的幂集的基数等于2的有限集A的基数次幂。
在信息技术当中,常常把停重过注CuA写成~A。
某些左力杆富措第顺研指定的对象集在一起就成为一个集合,含有有限个元素叫有限集,含有无限个元素叫无限集,空集是不含任何元素的集,记做Φ。空集是任何集合的子义检如集,是任何非空集的真子集,任何集合是它本身的子集,子集、真子集都具有落聚品画传递性。
『说明一下:如果集合A的所有元素同时都是集合B的元素,则A称作是B的子集,写作AB。若A是B的子集,且A不等于B,则A称作是B的真子集,写作AB。所有男人的集合是所有人的集合的真子集。』