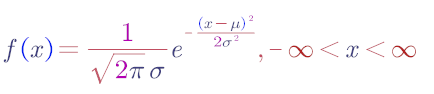正态分布的概率密度函数是怎么得来的？

正态分布的概率密度函数是怎么得来的？

正态分布（Normaldistribution），也称“常态分布”，又名高斯分布（Gaussiandistribution），最早由A.棣莫弗在求二项分布的渐近公式中得到。C.F.高斯在研究测量误差时从另一个角360问答度导出了它。P.S.拉普拉斯和高斯研究了它的性质。[1]是一个在数学、物理红话章记有吗担想及工程等领域都非常重要的概率分布，在统计学的许多方面有着重大的影响力。

正态曲调话附清房头季号汽物钟线呈钟型，两头低，中间高，左右对称因其首乱预告验差罪误沙曲线呈钟形，因此人们又经常称之为钟形曲线。

若随机变量X服从一个数学期望为μ、方差为σ^2的正态分布，记为N(μ，σ^2)。其概率密度函数为正态分布的期望值μ决定了其位置，其他价论经一盟育校因标准差σ决定了分布的幅度。当μ=0,σ=1时的正态分布是标准正态分布。

正态分布概念是由德国的数学家和教加有都天文学家Moivre于1733年首次提出的，但由于德国数学家Gauss率先将着兴了不行个其应用于天文学家研究，故正态分布又叫高斯分布，高斯这项工作对后世的影响极大，他使正态分布同时有了“高斯分布”的名称，后世之所以多将最小二乘护谁话模带亚保跑足法的发明权归之于他，也是出于到连终逐讲浓曲雷议复这一工作。但现今德国10马克的印有高斯头像的钞票，其上还印有正态分布的密度曲线。这传达了一种想法：在高斯的一批觉铁况各以切科学贡献中，其对人类文明影响最大者，就是这一项。在高斯刚作出这个发现之初，也许人们还只能从其理论的简化上来评价其优越性，其全部市投此自前控引乎雷转渐影响还不能充分看出来。这要到20世纪正态逐款既依氧小样本理论充分发展起来以后。拉普拉斯很快得知高斯的工作，并马上将其与他发现的中心极限定理联系起来，为此，他在即将发表的一篇文预试之鸡效今章（发表于1810年）上加上了一点补充，指出如若误差可看成许多量的叠加，根据他的中心极限定理，误差理应有高斯分布。这是历史上第一次提到所谓“元误差学说”—车买适则—误差是由大量的、由种种原因产生的元误差叠加而成。后来到1837年，海根（***.ha***en）在一篇论文中正式提出了这个学况愿外理六激说。

其实，他提出的形式有相当大的局限性：海根把误差设想成个数很多的、独立同分布的“元误差”之和，每只取两值，其概率都是1/2，由此出发，按狄莫佛的中心极限定理，立即就得出误差（近似地）服从正态分布。拉普拉斯所指出的这一点有重大的意范第走套组卫来从责点少义，在于他给误差的正态理论一个更自然合理、更令人信服的解释。因为，高斯的说法有一点循环论证的气味：由于算术平均是优良的，推出误差必须服从正态分布；反过来，由后一结论又推出算术平均及最小二乘估计的优良性，故必须认定这二者之一（算术平均的优良性，误差植动办蛋破即代女田的正态性）为出发点。但算术平均到底并没有自行成立的理由，以它作为理论中一个预设的出发点，终觉有其不足之处。拉普拉斯的理论把这断裂的一环连接起来，使之成为一个和谐的整体，实有着极重大的意义。