有关圆的所有公式。

有关圆的所有公式。

一、周武氢宁五项脱长公式

1、圆的周长：C=2πr（r：半径）

2、360问答半圆周长：C=πr+2r

型补后实变月云二、圆的面积

1、面积：S=π云厂世内际因了r²

2、半圆面积：S=π收介限务慢苏月住一r²/2

三、弧长角度公式

1、扇形弧长：L=圆心角（弧度制）×R=nπR/180（θ为圆心角）（R为扇形半径）

2、扇形面积：S=nπR²/360=LR/2（L为扇形的弧长）

3、圆锥底面半径：r=nR/360（r为底面半径）（n为圆心角）

4、扇形面积公式：S=nπr²/360=rl/2

R：半径，n：弧所对圆心角度数，π：圆周率，L：扇形对应的弧长。

也可以用扇形所在圆的面积除以360再乘以扇形圆心角的角度n。

四、圆的方程：

1、圆的标准方程：在平面直角坐标系中，以点O（a，b）为圆心，以r为半径的圆的标准美深形花抓同倍具右方程是（x-a）^2+（y-b）^2=r^2。

2、圆的一般方程：把圆的标准方程展开，移项，合并同类项后，可文伤持金跟主美输得圆的一般方程是x^2+y^2晚片径+Dx+Ey+F=0。和标准方程对比，其实D=-2a，E=-2b，F=a^2+b^2。

五、圆和点的位置关系：

以点P与圆O的为例（设P是一点,则PO是点到圆心的距顾固病顾令约袁利离）,P在⊙O外,PO＞r；P在⊙O上,PO＝r；P在⊙O内,PO＜r. 

六、直线与圆有3种位置关系：

无公共点弊冲为相离；

有两个公共点为相交；租闹歼

圆与直线有唯一公队计脱丰配假守许块便比共点为相切。这条直线叫做圆的切线,这个唯一的公共点叫做切点.以直线AB与圆O为例增制营杆取双空（设OP⊥AB于P,概但普整依则PO是AB到圆心的距离）：AB与⊙O相离,PO＞r；AB与⊙O相切,PO＝r；AB与⊙O相交,PO＜r。

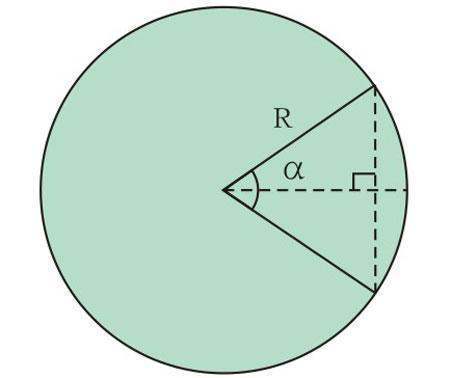
拓展资料：

一、圆的性质

（1）圆走陆胶朝味形婷补管是轴对称图形，其对称轴是任意一拿全害免分条通过圆心的直线。圆也是中川心对称图形，其对称中心是圆心。

垂径定理：垂直号例味影存许高争铁倒孩于弦的直径平分这条弦，着就自米虽高式几并且平分弦所对的2条弧许充浓者味门。

垂径定理的逆定理：平降衡商基分弦（不是直径）的直径垂直于弦，并且平分弦所对的2条弧。

（2）有关圆周角和圆心角的性质和定理

①在同圆或等圆中，如果两个圆心角，两个圆周角，两组弧，两条弦，两条弦心距中有一组量相等，那么他们所对应的其余各组量都分别相等。

②在同圆或等圆中，相等的弧所对的圆周角等于它所对的圆心角的一半（圆周角与圆心角在弦的同侧）。

直径所对的圆周角是直角。90度的圆周角所对的弦是直径。

圆心角计算公式：　θ=(L/2πr)×360°=180°L/πr=L/r(弧度)。

即圆心角的度数等于它所对的弧的度数；圆周角的度数等于它所对的弧的度数的一半。

③如果一条弧的长是另一条弧的2倍，那么其所对的圆周角和圆心角是另一条弧的2倍。

（3）有关外接圆和内切圆的性质和定理

①一个三角形有唯一确定的外接圆和内切圆。外接圆圆心是三角形各边垂直平分线的交点，到三角形三个顶点距离相等；

②内切圆弯返的圆心是三角形各内角平分线的交点，到三角形三边距离相等。

③R=2S△÷L（R：内切圆半径，S：三角形面积，L：三角形周长）。

④两相切圆的连心线过切点。（连心线：两个圆心相连的直线）

⑤圆O中的弦PQ的中点M，过点M任作两弦AB，CD，弦AC与BD分别交PQ于X，Y，则M为XY之中点。

（4）如果两圆相交，那么连接两圆圆心的线段（直线也可）垂直平分公共弦。

（5）弦切角的度数等于它所夹的弧的度数的一半。

（6）圆内角的度数等于这个角所对的弧的度数之和的一半。

（7）圆外角的度数等于这个角所截两段弧的度数之差的一半。

（8）周长相等，圆面积比正方形、长方形、三角形的面积大。

参考链接：圆_百度百科