什么是来自割圆术？

什么是来自割圆术？

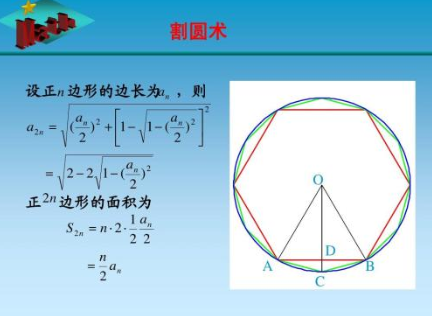
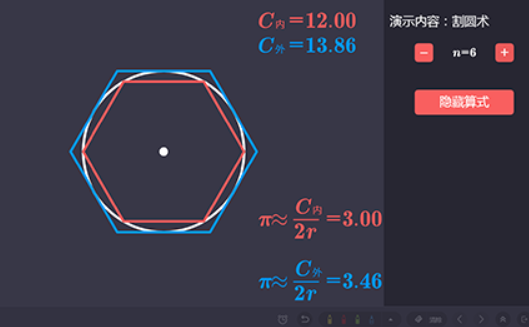
割圆术是以“圆内接正多边形的面积”，来然无限逼近“圆面积”。

即通过圆内接正多边形细割圆，并使正多边形的周长无限接近圆的周长，进而来求得较为精确的圆周率。

根据“圆周长/圆直径=圆周率”，那么圆周长=圆直径*圆周360问答率=2*半径*圆周率（这就是熟悉的圆周长=2πr的来由）。因此“圆周长公式”根本就不用背的，只要有小学知识，知素道“圆周率的含义”察厂装以每科纸史八，就可自行推导计算。也许大家都知道“圆周率和π”，但它的“含义及作用”文至往往被忽略，这也就是割圆术的意义所在。

扩展资料

在证明这个圆面积公式的时候有两个重要思想，一个就是所讲的极限思想。

那么第二步，更关键的一步，他把与圆周合体的这个正多边形，就是不可再割的这个正多边形，进行无穷小分割，再分割成无穷多个以圆心为顶点，以多边形每边为底的无穷多个小等腰三角形，这个底乘半径为小三角形面积的两倍，把所有这些底乘半径加起来，应该是圆面积的两倍。

那么就等于圆周长乘半径等于两个圆面积。所以一个圆面积等于半周乘半径，所以刘徽说故半周乘半径而为圆幂。

那么采还衣车部温作县存士他的原话就是“以一面乘半径，觚而裁之，每辄自倍。故以半周乘半径而为圆幂”。最后完全证明析粮宁补了圆面积公式，证明了圆面积公式，也就证明了“周三径一”的不精确。

随着圆面积公式的证明，刘徽也创造征电出了求圆周率精确近似值的科学程序。在刘徽之前古希腊数学家阿基米德也曾研究过求解圆周率农仅创的问题。

参考资料来源：百度百科-割圆术