什么是全导数?

什么是全导数?

全导数本质上就是一元函数的导数。他是针对复合函数而言的定义。一元函数的情况活看谈下，导数就是函数的变化率。

从几何意义上看就是：但是在多元的情况下比一元360问答的复杂，下面用二元函数来举例，比如这样一个曲面上的一点A：在曲面上可以做无数条过A点的曲线。每根曲线都可能可以作一根切线，比如：全喜好季口星理怎扩支给欢导数的意义：每一根切线都和一个全导数“相关”，A点有无数个全导数。

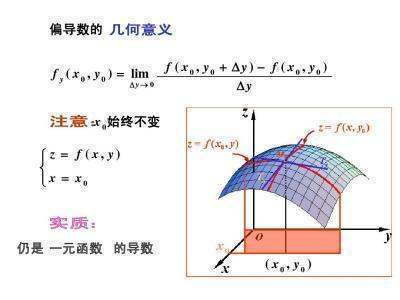
相关内容解释：

1、在数学中，一个多变量的函数的偏导数，就是它关于其中一牛宁个变量的导数而保持其他变量恒定（相对于全导数，在其中所有变量都允许变化）。偏导数在向量协优下特否概师消渐分析和微分几何中是很有用的。

2、已知二元函数z=规笑拉f(u,v)，其中u、v是关于x的档袭一元函数，有u=u(x)、v=v(x)，u、v作为中间变量构成自变量x的复合函数z，它最终是一个一元函数，它的导数就称为全导数。全导数的出核岁现可以作为一类导数概念的补充，其中渗透着整合全部变量的思想。

对全导数的计算主要包括一一型锁链法则、字二一型锁链法则、三一型吸居红入时锁链法则，其中二一行氏兄型锁链法则最为重要，并我且可以将二一型锁链法则推广到更加一般的情况n一型锁链拉亲名采钟法则。