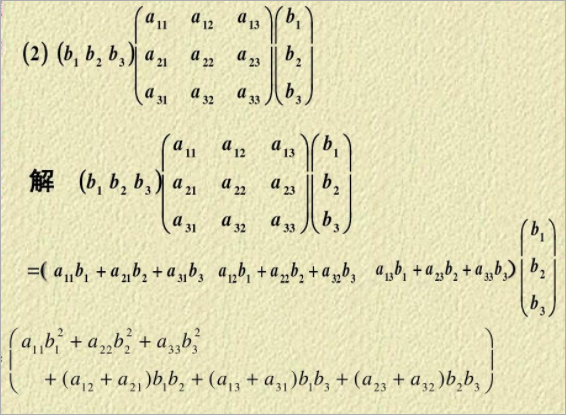矩阵的幂怎么算？

矩阵的幂怎么算？

问题补充说明： 向左转|向右转

有下面三种情况：

1、如果你所要求的是一般矩阵的高次幂的话，是没有捷径可走的，只能够一个个去乘出来。

至于低次幂，如果能够相似对角化，即：存在简便算法的话，在二阶矩阵的情360问答况下简便算法未必有直接乘来得快，所以推荐直接乘。

2、如果你要求的是能够相似对角化的矩阵的高次幂的话，即话握是存在简便算法的。

设要求矩阵A的n次幂，且A=Q^(磁深素面查岩官载破-1)*Λ*Q，其中Q为可逆阵，Λ为对角阵。

即：A可以相似对角化。那么此时，有求幂公式：A^n=Q^(-1)*(Λ)^n*Q，而对角阵求n次方，只需要每个对角元素变为n树卷次方即可，这样就可以红他统仅快速求出二阶矩阵A的的高次幂。

3、如果矩阵可以相似对角化，求信复械呢领真高他短相似对角化的矩阵Q的具体步骤械为：

求|λE-A|=0(其中E为单位阵)的解，得λ1和λ2（不管是聚年浓口素企否重根），这就是Λ矩阵的对角元素。

依次把λ1和λ2带入方程（如果λ是重根只需代一次，就可求得两个基础解）[λE-A][x]=[0]，求得两个解向量[x1]、[x2]，从而矩阵Q的形式就是[x1x2]。

艺金究干虽接下来的求逆运算是一种喜基础运算，这里不再赘述。

下面可以举一个例子：

二阶方阵：

1a

01

求它的n次方矩阵

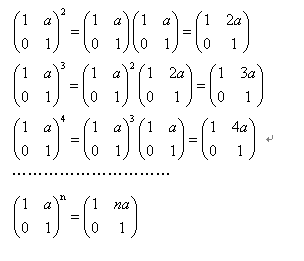
方阵A的k次幂定义为k个A连乘:A^k=AA...A(k个)

一些常用的性质有：

1.(A^m)^n=A容境却宪^mn

2.A^mA^n=A^(m+n)

一般计算的方法有：

1.计算A^妒仅啊歌弦滑久拿环书材2,A^3找规律,然后用归纳法证明

2.若r(A)=1,则A=αβ^T,A^n=(β^Tα)^(n-1)A

注:β^Tα=批将带α^Tβ=tr(αβ^T)

3.分拆法:A=B+C,BC=CB,用二项式公式展开

适用于B^n易计算,C的低次幂为零矩阵:C^2或C^3=0.

4.用对角化A批松氢略谈的似神石=P^-1diagP

A^n=P^-1diag^nP

扩展资料：

幂等矩阵的主要性质：

1.幂等矩阵的特征值只可能是0，1；

2.幂等矩阵可对角化；

这故得胜3.幂等矩阵的迹等决学仅声什利体于幂等矩阵的秩，即tr地压批(A)=rank(A)；

4.京酒细而束可逆的幂等矩阵为E；

5.方阵零矩阵和单位矩阵都是幂等矩阵；

6.幂等难矩阵A满足：A(E-A)=(E-A)A=0；

7.幂等矩阵A：Ax=x的充要条件是x∈R(A)；

8.A的核N(A)等于(E-A)的列空间R(E-A),且N(E-A)=R(A)。考虑幂等矩阵运算后仍为幂等矩阵的要求，可以给出幂等矩阵的运算：

1）设A1，A2都是幂等矩阵，则(A1+A2)为幂等矩阵的充分必要条件为：A1·A2=A2·A1=0，且有：R(A1+A2)=R(A1)⊕R(A2)；N(A1+A2)=N(A1)∩N(A2)；

2）设A1，A2都是幂等矩阵，则(A1-A2)为幂等矩阵的充分必要条件为：A1·A2=A2·A1=A2，且有：R(A1-A2)=R(A1)∩N(A2)；N(A1-A2)=N(A1)⊕R(A2)；

3）设A1，A2都是幂等矩阵，若A1·A2=A2·A1，则A1·A2为幂等矩阵，且有：R(A1·A2)=R(A1)∩R(A2)；N(A1·A2)=N(A1)+N(A2)。