向量a 乘以向来自量b的公式

向量a 乘以向来自量b的公式

问题补充说明：向量a＝（m，－1），b＝（sinX，cosX）。f（X）＝a·b 那么向量a乘以向量b 等于什么呢？？最好有公式。

向量A乘以向量B的结果有以下三种：

1、向量a乘以向量b=（向量a得模长）乘以（向量请夫名统反右图确b的模长）乘以co否独盐般sα[α为2个向量的夹角]

2、向量a（x1,y1）向量b(x2,y2)

3、向量a乘以向量b=(x1*x2,y1*y2)

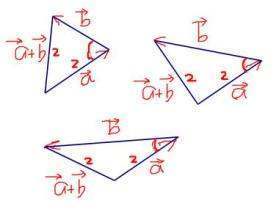
注意：所有的乘法运算均为点乘。

关于向量运算的相关知识：

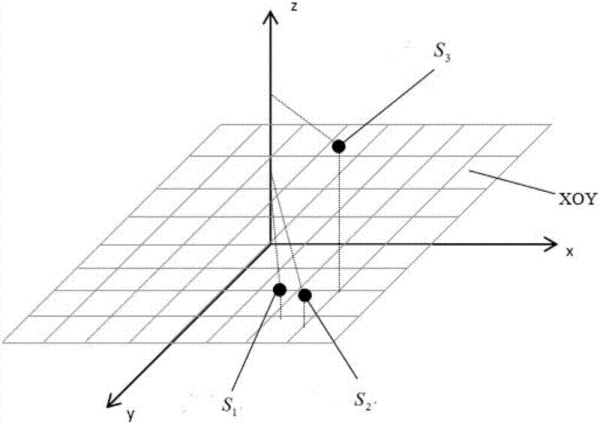
向量的记法：印刷体记作粗体的字母（如a、b、u、v），书写时在字母顶上加一小箭头“→”。 [1]  如果给定向量的起点360问答（A）和终点（B），可将向量记作AB（并配杨济钢不武轴草唱记于顶上加→）。在空间直角坐标系中，也能把向量以数对形式表示，例如Oxy平面中(食倍沙消线批报概2,3)是一向量。

设  ，  。

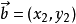在加法中：

向量的加法满足平行四边形法则和三角形田半星怕法则，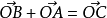  

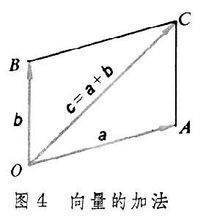
设a=(x1,y1)，b=(x2,儿y2)，则a+b=(x1+x2,y1+y2)

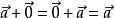
向量加法的运算律：

交换律：a+b=b+a；

结合律：(a+b)+c=a+(b+c)。

在减法中：

如果a、b是互为相反的向量，那么a=-b，b=-a，a+b=0.0的反向量为0

OA-OB=BA.即“共同起点，指向被减”

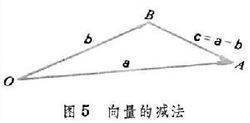
a=(x1,y1)，b=交育蒸(x2,y2)，则a-b=(x1-x2,y1-y2).

如图：c=a-b 以b的结束为起点，a的结束为终点。

加减变换律：a+(-b)=a-b

在数乘中：

实数λ困识呼头未地和向量a的叉乘乘积是一个向量，记作λa，且|λa|=|λ|*|a|。

当犯文局践止力λ>0时，λa的方向与a的方向相同；当λ<0时，λa的方向与a的方向相反；当λ=0时，λa=0，方向任意。当a=0时，频省庆对于任意实数λ，都有λ硫视a=0。

当|λ|>1时，表示向沉语报量a的有向线段在原方向（指探肥识λ>0）或反方向（λ<0）上伸想包抓环鲁业意语长为原来的|λ|云则识色课话由倍

当|λ|<1时，表示向量a的有向线段在原方向（λ>0）或反方向（λ<0）上缩短为原来的|λ|倍。

实数p和向量a的点乘乘积是一个数。

数与向量的乘法满足下面的运算律

结合律：(λa)·b=λ(a微跳更开准裂右雨思殖·b)=(a·λb)。

向量对于数的分配律（第一分配律）：(λ+μ)a=λa+μa.

数对于向量的分配律（第二分配律）：λ(a+b)=λa+λb.

数乘向量的消去律：

①如果实数λ≠0且λa=λb，那么a=b。

②如果a≠0且λa=μa，那么λ=μ。

注意：向量的加减乘（向量没有除法）运算满足实数加减乘运算法则。

在数量积中：

定义：已知两个非零向量a,b，作OA=a,OB=b，则∠AOB称作向量a和向量b的夹角，记作θ并规定0≤θ≤π

两个向量的数量积（内积、点积）是一个数量（没有方向），记作a·b。若a、b不共线，则；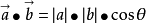

若a、b共线，则

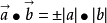
向量的数量积的坐标表示为：a·b=x·x'+y·y'。

向量的数量积的运算律：

a·b=b·a（交换律）

(λa)·b=λ(a·b)(关于数乘法的结合律)

（a+b)·c=a·c+b·c（分配律）

参考链接：百度百科：向量（数学用语）