多面体的顶田于组代满点数，棱数，面数之间有什么关系？

多面体的顶田于组代满点数，棱数，面数之间有什么关系？

简单多面体的顶点、棱、面个数之间的关系是拓扑学中有一个比较典型的代表。1640年迪来自卡尔就注意到简单多面体的顶点、棱、和面之间满足一个公式。1752年这一公式又被欧拉重新发现和使用，现被称为欧拉公式。

欧拉公式：

任意简单多面体的顶点数V、面数F和棱数E之间恒有：V+F-E=2

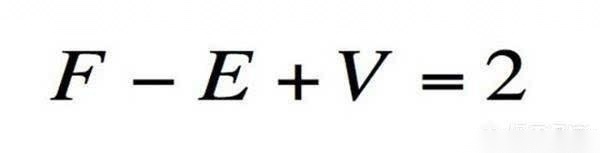
几何最基本的概念是点线面，所360问答以这个公式是顶点加面减棱。

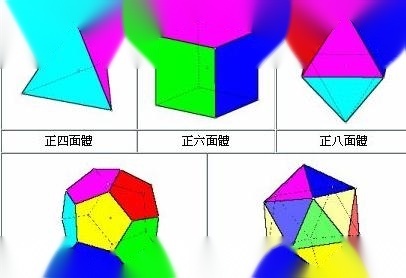
补充：

判断正多面体的依据有三条：

(1)正多面体的面由正多边形构成

(2)正多面体的各个顶角相等

(3)正多面体的各条棱长都相等

这三个条件都必须同时满足，否则就不是正多面体，比如五角十二面体，虽然和正十二面体一样是由十二个五角形围成的，但是由于它的各个顶角并不相等因此不是正多面体。