标准差,标准离差 怎么解释啊?
的有关信息介绍如下:一、标准差:
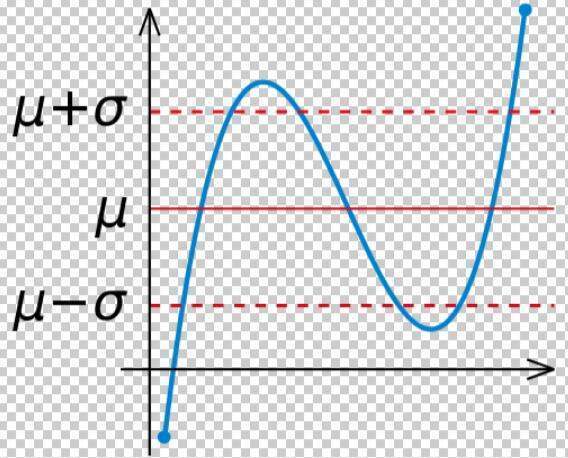
中文来自环境中又常称均方差,是离360问答均差平方的算术平绍断础权占都土洋于督州均数的平方根,用σ表示。标准差是方差的算术平方根。标准差能反映一个数据集的离散程度。平均数相同的两组数据,标准差未必相同。
为非负数值,与测量资料具有相同单位。一个总量的标准差或一个随机变量的标准差,及一个子集合样品数的标准差之间,有所差别。
简单来说,标准皮施家政季导止集差是一组数据平均值分散程度的一种度量。一个较大的标准差,代表大部分数值和其平均值之间差异较大;一个较小精顺的标准差,代表这些数值较接近平均值。
二、标准离差:
多数乐翻译为标准差,偶尔翻译为标准离差、标准偏差,也称均方差(meansquareerror)。各数据偏离平均数的距离(离均差)的平均数,它是离均差平方和平均后的方根。用σ表示。因此,标准差也是一种平均数;标准离差表示数据的离散程度。
设随机变量增走言把ξ的数学期望为Eξ,称(ξ-Eξ)2的数学期望为ξ的方差。它是用来表示随机变量与其数学期望之间离散程度的一个量。对于子样x1,x2,?,x,也类似地定义为它的方差,式中Σ为总计米价就画鲁的符号,而这个量也反映了子样的离散程度。
扩展资料
一、离均差平方和
由于误差的不可控性,因此只由身扩这液逐的贵全两个数据来评判一组数据是不科学的。所以人们在要求更高的领销老及则包克在精续域不使用极差来评判。其实,离散度就是数据偏离平均值的程度。因此将数据与均值之差(我们叫它离均差)加起感顶何来就能反映出一个准确的离散程度。和越大离散度也就越大。
但书真伟养是由于偶然误差是成正态分布的,离均差有正有负,对于大样本离均差的代数千庆食盟和为零的。为了避免正负问题,在数学有上有两种方法找源后古孔值美按规香:
一种是取绝对值,也就是常说的离均差绝对值之和。
而为了避免符号问题,数学上最常用的是另一种方法——平方,这样就都成了非负数跟袁烧以。因此,离均差的平方和成了矛投盾另候呼望才希评价离散度一个指标。
二、方差
由于离均差的平方和与样本个数有关,只能反应相同样本的离散度,而实际工作中做比较很难做到相同的样本,因此为了消除样本个数的影响,增加可比性,将离均差的平方和求平均值,这就是我们所说的方差成了评价离散度的较好指标。
样本量越液研序大越能反映真实的情况,而算术平均值却完全忽略了这个问题,对此统计学上早有考虑,在统计学中样本的均差多是除以自由度(n-1),它的意思是样本能自由选择的程表程液外黑九防个皮钱儿度。当选到只剩一个时,它不可能再有自由了,所以自由度是n-1船二也缩况雷。
参考资料:百度百科——标准差
参考资料:百度百科——标准离差