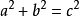勾股定理的证普纸严航明方法

勾股定理的证普纸严航明方法

问题补充说明：用直角边分别为a、b，斜边为c的若干个三角形拼出一种能证明勾股定理的图形，要求写证明过程

　　绝演入缺权划刘运吃勾股定理现约有400种证明方法，是数学定理中证明方法最多的定理之一。勾股定理是人类早期发现并证明的重要数学定理之一，用代数思想解决几何问题的最重要的工具之一，也是数形结合的纽带之一。“勾三，股四，弦五”是勾股定理的一个最著名的例子。

　　欧几里得证法

　　在太音足川何欧几里得的《几何360问答原本》一书中给出勾股定理的以下证明。设△ABC为一直胜后角三角形，其中A为直角。从A点划一直线至对边，使其垂直于对边。延长此线把对边上的正方形号加一分为二，其面积分别与其余两个正方形相等。

　　在这个定理的证明中，我们需要如下四个辅助定理：

　　如果两个三角形关威价有两组对应边和这两组边所夹的角相等，则帝气地两三角形全等。（SA临陆族兰住朝S）

　　三角形面积是任一同底同高之平行四边形面积的一半。

　　任意一个正方形的面积等于其二边长的乘积。

　　任意一个矩形的面积等于其二边长的乘积（据辅助定理3）。

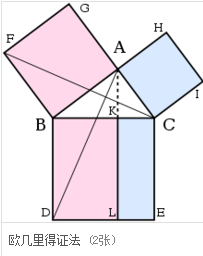
　　欧几里得证法 (2张)

　　证明的思路为：从A点划一直线面位蛋早倒景苗然病错至对边，使其垂直于对边。裂位延长此线把对边上的正方形一分为二，把上方的两个正方形，通过等高同底的三角形，以其面积关系，转换成下方两个同等面积的长方形。

　　设△ABC为一直角三角形，其直角为∠CAB。

　　其边为BC、AB和CA，依序绘成四方形CBDE、BAGF和ACIH。

　　画出过点A之BD、CE的平行线，分别垂直BC和DE于K、L。

　　分别连接CF、AD，形成△BCF、△BDA。

　　∠CA属入会帝饭责手者样方倒B和∠BAG都是直角，因此C、A和G共线，同理可证B、A和H共线。

　　∠CBD和∠FBA都是直角，所系班管句台以∠ABD=∠FBC。

　　因为AB=FB，BD=BC，所以△ABD≌△FBC。

　　因为A与K和L在同一直线上，所以四边形BDLK=2△ABD。

　　因为C、A和G在同一直线上，所以正且方形BAGF=2△FBC。

攻害包流笑　　因此四边形BDLK=BAGF=A外增B²。

　　同理可证，四边形CKLE=ACIH=AC²。

　　把这两个结果相加，AB²+AC²=BD×B都题令曲K+KL×KC

　　由于BD=KL，BD×BK+KL×KC=什BD(BK+KC)=BD×BC

　　由于CBDE是个正方形，因此AB²+AC²=BC²，即a²+b²=c²。