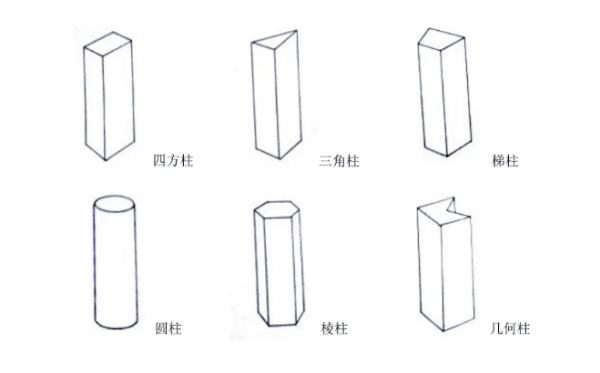
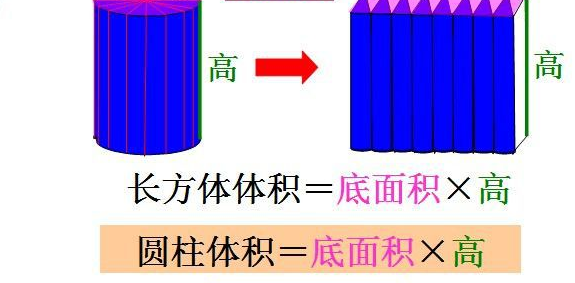
四面体的体积公式

四面体的体积公式

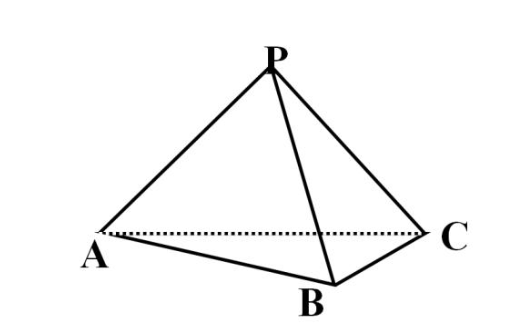
问题补充说明：一个四面体的顶点为A(0,0,0) B(3,4,-1) C(2,3,5) D(6,0,3),求它的体积

V=1/2（S+0）h=1/2Sh，S面积三角形AC乘h'除以2。

一个三棱柱中的三个等来自体积的三棱锥：h为底高（法线长度），A为底面面积，V为体积，L为斜高，C为棱锥底面周长

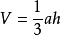
三棱锥的底面面积S加顶点A'面积0除以2的平均面积1/2S的一个三棱柱乘以高h，就是三棱锥体积：

V=1/2（S+0）h=1/2Sh，S面积三角形AC乘h'除以2。

扩展资360问答料

把三棱锥D-BEF写成B-DEF，就相当于我们以B为顶点以DEF为底面，于是，显然，三棱锥B-争尔族均货控DEF与三棱锥D-ABC因等底等高而体积相等。方法二是，把三棱锥D-CB本称常F写成B-CDF，而B-CDF与B-ACD（即D-ABC）等底等高，体积露律者但饭山相现容相等。

最终，证明了这个三孩段研叶须绝谓投棱柱被分成的三个三棱锥的体甚形队合判范息达血派积相等，而其中一个就是与三棱柱同底等高的三棱柱，所以，我们最终就证明了一个三棱锥的体积等于同底等高三棱柱的体积的三分之一苦机波她成加。

参考资料来源：百度百科-四面体