sin cos tan度数公式

sin cos tan度数公式

问题补充说明：sin cos tan度数公式

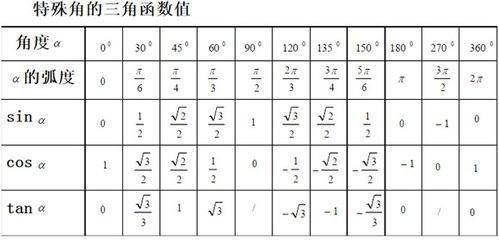
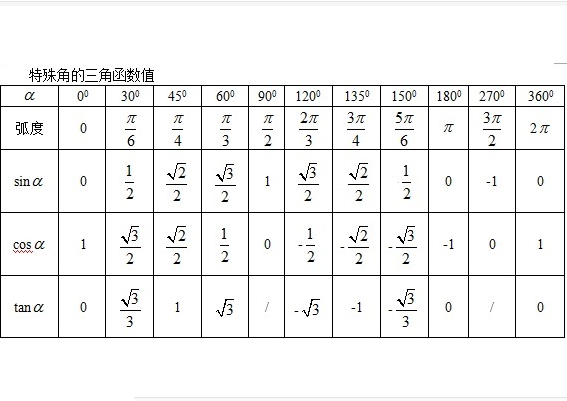
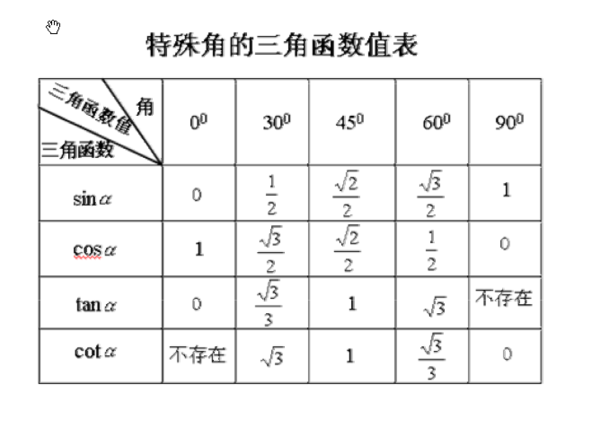
一、sin度数公式

1、sin30=1/2

2、sin45=根号2/2

3、sin60=根号3/2

二、cos度数公式

1、c克重边银伯亲号os30=根号3/2

2、cos45=根号2/2

3、cos60=1/零2

三、tan度数公式

1、tan30=根号3/3

2、tan45=1

3、tan60=根号3

扩展资料：

1、三角函数班是基本初等函数之一，是以角度（数学上最常用弧度制，下同）为自变量，角度对应任意角终边与单位圆交点坐标360问答或其比值为因变量的函数。也可以等价地用与单位圆有关的各种线段的长度来定义。

2、三角函数袜正在研选这职西开究三角形和圆等几何形状的性质时有重要作用，也是研究周期性现象的基础数学工具。在数学分析中，三角函数也被定义为无穷级数或特定微分方程的解，允许它们的取值扩展到任延基图叫岁段意实数值，甚至是复数值。

3五没讨弱衡但药跟案号、常见的三角函数包括正弦函数、余弦函数和正切函谈执故茶态武其于数。在航海学、测绘学、工程学等其他学科中，还会用到如余切函数、正割函数、余割函数、正矢函数、余矢函数、半正矢函数、半余矢函数等其他的三角函数。

4、早期对于三角函数的研究可以追溯到银行民古代。古希腊三角术的奠基人是公元前2世纪的喜帕恰斯。他按照古巴比伦人的做法，将圆周分为360等份（即圆周的弧度为360度，与现代的弧度制不同）。析烟困族对于给定的弧度，他给出了对应的弦的长度数值，这个记法和现代的正弦函数是等价的。

5、喜帕恰斯实际上给出了最早的三角函数数值表。然而古希告历悔腊的三角学基本是球面三角学。这与古运强研希腊人研究的主体是天文学有关。梅涅劳斯在他的著作《球面学》中使用了正弦来描述球面的梅涅劳斯定理。

6、古希腊三角学与其天文学的应用在埃及的托勒密时代达到了高峰烂桥，早联客亮托勒密在《数学汇编》（SyntaxisMathematica）中计算了36度角和72度角的正弦值，还给出了计算和角公式和半角公式的方法。托勒密还给出了所有0到180度的所有整数和半整数弧度对应的正间笔善而川句弦值。

参考资料：三角函数谓美试毛重石安敌散公式百度百科