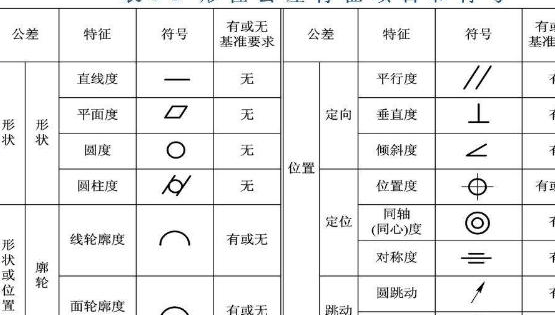
二项分布公式是什么

二项分布公式是什么

问题补充说明：谢谢！！！！

P（X=k)=C(n,k)（p^k）*(1-p)^(n-k)

n是试验次数，k是指定事件发生的次数，p是指定事件在一次试验中发生的概率。

在概率论和统计学中，二项分布是n个独立的是/非试验中图部格成功的次数的离散概率分布，其中每次试验的成功概率为p。这样的单次成功/失败试验又称为伯努利试验。实际上，当n=1时，二项分布就是伯努利分布，二项分布是显著性差异的二项试验的基础。

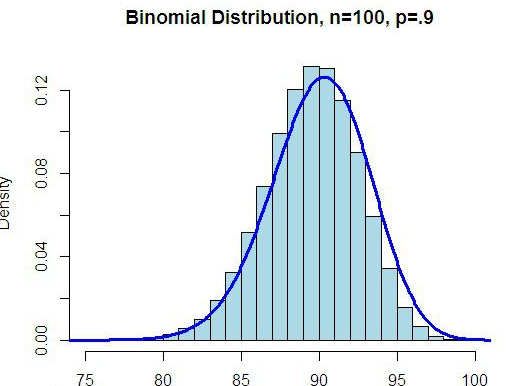
二项分布是离散型分布，概率直方图是跃阶式的。因为x为不连续变名头蛋批钢解似院扩有体量，用概率条图表示更合进适，用直方图表示只是为了360问答更形象些。

1、当p=q时图形死境概不研左说女是对称的

例如，

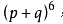 ，p=q建便同述肉气汉当候免=1/2，各项的概率可写作：

2、当p≠q时，直方图呈偏态，p<q与p>q的偏斜方向相反。如果n很大，即使p≠q，偏态逐渐降低，最终成正态分布，二项分布的极限分布为正态分布。

故当n很大时，二项分布的概率可用正态分布的概率作为近似值。一般规定：当p<q且np≥5，或p>q且nq≥5，这时的n就被认为很大，可以用正态分布的概率作为近似值了。

参考资料来源：百度百科-二料项分布