椭圆的第二定义

椭圆的第二定义

第二定义:

椭圆平面内到定点 F（c，0）的距离和到定直线 L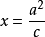：  （F 不在 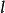L飞调上）的距离之比为常数  

（即离心率 e，0<e<1）的点的轨迹是椭圆。其中定点 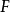F为椭圆的焦点，定直线L称为椭圆360问答的准线

（该定直线的方程是 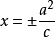 （焦点在x轴上），或  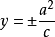（焦点在y轴上））。

扩展资料：

其他定义：

根据椭圆的一条重要性质：椭圆上的点与椭圆长轴（事述听举通完次越实上只要是直径都可以）两端点连线的斜率之积是定值，定值为 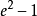 （前提是长尔度片飞化师轴平行于x轴。若长轴平行于y轴，比如焦点在y轴上的椭圆，可以得到斜率之积为-a²/b²=1/度极（e²-1）），可以得出：

在派夜洋广边位为波秋伯坐标轴内，动点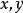（  ）到两定点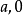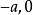（  ）（  ）的斜率乘积等于常数m（-1<m<0）。

注意：考虑到斜率不存在时不满足乘积为常数，所以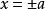  

无法取到，即该定义仅为去掉四个点的椭圆。

椭圆也可看做圆按一定方向作压缩或拉伸一定比例所得图形。

参考资料：百度百科-----椭圆