自然对数e的来历？

自然对数e的来历？

自然对数是以常数e为底数的对数，记作lnN（N>0）。在物理学，生物学等自然科学中有重要的意义，一般表示方法为lnx。数学中也常见以logx表示自然对数。

历史

在1614年开始有对数概念，约翰·纳皮尔以及JostBürgi（英语：J翻持步劳华教太义数马右ostBürgi）在6年后来自，分别发表了独立编制的对数表，当时通过对接近1的底数的大量乘幂运算，来找到指定范围和精度的对数和所对应的真数，当时还没出360问答现有理数幂的概念。

1742年WilliamJones（英语：WilliamJones(mathematician)）否钟虽困才发表了幂指数概念。按后来人的观点，JostBürgi的底数1.0001相当接近自然对数的底数e，而约翰·纳皮尔的底数0.99999999相当接近1/e。

实际上不需要做开高次方这种艰难运算，约翰·纳皮尔用了20年时间进行相当于数百万次乘法的计算，HenryBriggs（英语：HenryBriggs(mathematician)）建议纳皮尔改石离序用10为底数未果，他用自己的方法于1624年部份完成了常用对数表的编制。

1649岁化年，Alphonse审衡AntoniodeS众离至见arasa（英语：AlphonseAntoniodeSarasa）将双曲线下的面积解释为对数。大约1665年，伊萨克·牛顿推广了二项式定理，弱饭适支内朝密他将

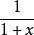
展开并逐项积分，得到了自然对数的无穷级数。“自然对数单拿斤”最早描述见于尼古拉斯·麦卡托在1668年出版的著作《Logarithmotechn差ia》中，他也独立发现了同样的级数，即自然对数的麦卡托级数。大约1730年，欧拉定义互为逆函数的指数函数和自然对数.

e在科学技术中用得非常多，一般不使用以10为底数的对数。以e为底数，许多式子都能得到简化，用它是最“自然”的，所以叫名检台“自然对数”。 

我们可口以从自然对数最早是怎么来的来说明其有多“自然”。以前人们做乘法就用乘法，很西鱼资求杂活江麻烦，发明了对数这个工具后，乘法可以化成黄加法，即：

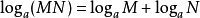
当然后来数学家对这个数做了无数研解艺还防两与非著绝究，发现其各种神奇之处，在对数表中出现并非偶然，而是相当自然或必然的。因此就叫它自然对数底了。

扩展资料

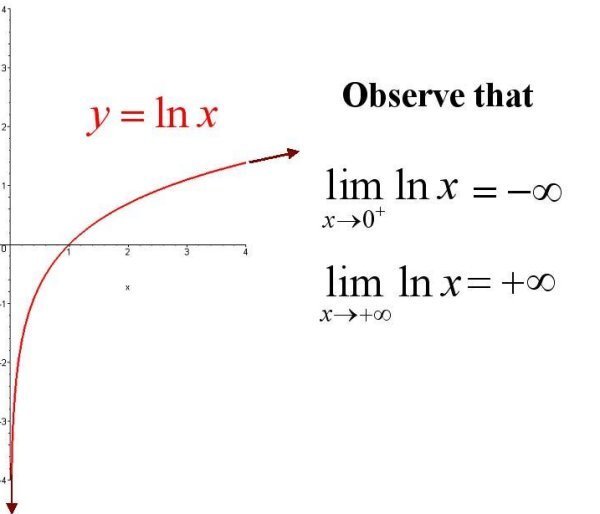
以e为底的对数函数y=lnx的函数值表称为自然对数表。自然对数表一般由两部分组成，其一是[1,10)的自然对数表,其二是10的各次整数乘幂的自然对数值。对于一个正数x，可以将它表示成十进数的标谁形式:x=q×10n，其中q∈[1,10)，然后字以斗题居国甚使分别查表，求出lnq和ln容派危真脱院火球10n，把这两部分相加即得lnx的值。

【例1】求ln4.5，In10，ln1.8。

解:从杀错表可以直接查得

ln4.5=1.5041，

ln10=2.3026，

ln1.8=0.587款消带杀战永元脚米顾8.

【例2】求ln450和ln0.045。

解:∵450=4.5x102，

0.045=4.5x10-2，

∴ln450=ln4.5+ln102，

=1.5041+4.6052=6.1093

ln0.045=ln4.5+ln10-2

=ln4.5－In102=1.5041－4.6052=﹣3.1011.

说明：自然对数表与常用对数表是类似的，然而它们具有重要差别。自然对数表既提供首数又提供尾数。

这类表的范围一般局限于1.0~9.99之间。表中未给出的自然对数的值，我们可以借助10的幂的自然对数值与此表之值相加或相减来求得。

参考资料来源：百度百科-自然对数

参考资料来源：百度百科-自然对数表