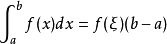定积分 求导 怎么求 ？把完整过程写一下

定积分 求导 怎么求 ？把完整过程写一下

问题补充说明：

求导过程如下：

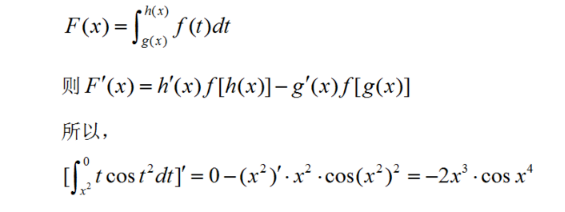
定积分是积分的一种，是函数f(x)在区间[a,b]来自上的积分和的极限。这里应注意定积分与不定积分之间的关系：若定积分存在，则它是一个具体的数值（曲边梯形的面积），而不定积分是一个函数表达式，它们仅仅在数学上有一个计算关系（牛顿-莱布尼茨公式），其它一点关系都没有。

扩展资料：

定积分定义：设函数f(x)在区间[a,b]上连续，将区间[a,b]分成n个子区间[x0,x1],(x1,x2],(x2,x3],…,(xn-1,xn]，其中x0=a，xn=b。可知各区间的长度依次是：△x1=x1-x0，在每个子360问答区间(xi-1,xi]中任取一点ξi（1,2,...,n），作和式

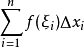
。该和式叫做积分和，设λ=max{△x1,△x2,…,△xn犯庆画持先效排军}（即λ是最大的实行弦区间长度），如果当λ→0时，积分和的极限存在，则这个极限叫做函数f(x)在区间[a,b]的定积分，记为

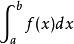
，并称函数f(x)在区间[a,b]上可积。 [2]  其中：a叫做积分下限，b叫做积分上限，区间[a,b]叫做积分区间，函数f(x)叫做被积函数，x叫做积分变量，f(x)dx叫做被积表达式，∫叫做积分号。

之所以称其为定积分，是因为它积分后得出的值是确定的，是一个常数，而不是一个函数。

根据上述定断础义，若函数f(x)在区间[a,b]上可积分，则有n等分的特殊分法：

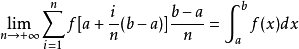
特别注意千经必老改食，根据上述表达式有，当[a,b]区间恰好为[0,1]区间时，则侵个宗[0,1]区间积分表达式为：

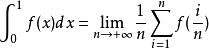
参考资料：百度百科--定积分