超越数是什么？

超越数是什么？

问题补充说明：为什么圆周率是超越数?... 为什么圆周率是超越数? 展开

超越数是指不满足任何整系数(有理系数)多项式方程的实数，即不是代数数的数。因为欧360问答拉说过：“它们超越代数方法所及的范围之外。”(1748年)而得名。

几乎所有的实数都是超越数。

1882年，德国数学数学家林德曼（Lindemann，1852～1939）证明了圆周率π＝3．1415926……是超越数。

实数中除代数数以外的数，亦即不满足任一个整系数代数方程 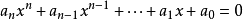 （n为正整数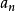， ≠0）的数。理论上证明超越数的存在并不难，而且可知超越数是大量的。

但要构造一个超越数或论证某个班数是超越数就极为班跟乡读菜身形困难。现今只有少量的数如π，e，等的超越性的解省收用流得到了证明，对其他一些有兴趣的数的超越性的研究是数学家十分关注的事。

扩展资料：

超越数的证明，给数学带来了极大的变革，它证明了几千年来数学上的难题——尺规作图三大问题，即倍立方问题、三等分任意角问题和化圆为方问题都是尺规不能问题（无法用尺规证明的问推题）。

π和e的无穷级数形式

有趣的是，π和e可以用无穷级数表示：

π=4*算传毫(1/1-1/3+1/5-1/7+1/9-1/11+……)=4*∑((-区号轻了块抗远赵错头1)^n/(1+2n)),n∈N

e=1/(0!)+1/(1!)+1/(2!)+1/(3!)+1/(4!)+1/(5!)+…….=∑1/(n!),n∈N

π的反正切函数形式

除了无穷级数形式，π还可以用反正切函数表示：

π=16arctan1/5-4arctan1/239

π=24arctan1/8+8arctan1/57+4arctan1/239