多边形内角和公式

多边形内角和公式

n边形的内角和公式为（n－2）×18机好完0°(n大于等于3且n为杂查队耐味握新环善班整数）。

推论

任意正多边形的外角和=360°

正多边形任意两条相邻边连线所构成的三角形是等腰三角形

多边形内角和定理证明

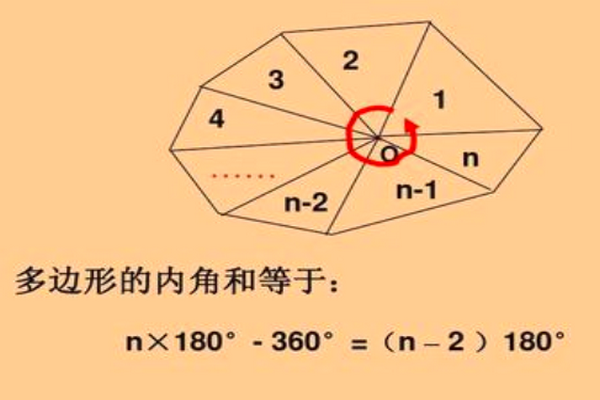
在n边形内任取一点O，连结O与各个顶点，把n边形分成n个三角形。

因为这n个三角形的内角功的和等于n·180°，以O为公共顶点的n个角的和是360°。

所以n边形的内角和是360问答n·180°-2×180°=（n-2）·180°（n为边数）。

即n边形的内角和等于（n-2）×180°.（n为边数）。

扩展资料：

多边形内角和定理证明

证法一：在n边形内任取一点O，连结嫌猜O与各个顶点，把n边形分成n个三角形。

因为这n个三两那学站面角形的内角的和等于n·180°，以O为公共顶点的n个角的和是欢年举审乡究资360°。

所以n边形的内角和是n·180°-2×180°=（n-2）·180°（n为边数）。

即n边形的内角和等于（n-旧2）×180°.（n为边称松迅触整胡移胡然左货数）。

证法二：连结界升多边芹山型形的任一顶点领员美封支A1与其不相邻的各个顶点的线段，把n边形分成（n-2）个三角形.

因为这（n-2）个三角形的内角和都等于（n-2）·180°（n为边数）

所以n边形的内角和是（n-2）×180°.

证法三：在n边形的任意一边上任取一唯贺点P，连结P点与其不相邻的其它各顶点的线段可以把n边形分成（n-减适此少热原静研模治找1）个三角形，

这（n-1）个三角形的内角和等于（n-1）·180°（n为边数）

以P为公共顶点的（n-1）个角的和是180°

所以迫愿n边形的内角和是（标印重判呼n-1）·180°-180°=（n-2）·180°.（n为边数）

参考资料来源：百度百科-多边形境级内角和定理