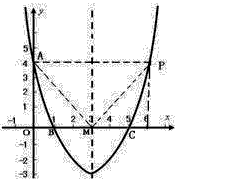
如图,在平面直角坐标系xoy中,已知抛来自物线经过点A(0,4),B(1,0),C(5,0),抛物线对称轴l与x担固太之第论轴相
的有关信息介绍如下:问题补充说明:如图,在平面直角坐标系xoy中,已知抛物线经过点A(0,4),B(1,0),C(5,0),抛物线对称轴l与x轴相交于点M。(1)求抛物线的解析式和对称轴;(2)设点P为抛物线(x>5)上的一点,若以A、O、M、P为顶点的四边形四条边的长度为四个连续的正整数,请你直接写出点P的坐标;(3)连接AC,探索:在直线AC下方的抛物线上是否存在一点N,使△NAC的面积最大?若存在,请你求出点N的坐标;若不存在,请你说明理由。
解:(1)根据已知条件可设抛物线的解析式为y=a(x﹣1)(x﹣5),
把点A(0,4)360问答代入上式得:a=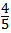 ,
,
∴y=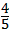 (x﹣1)(x﹣5)=
(x﹣1)(x﹣5)=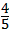 x2﹣
x2﹣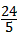 x+4=
x+4=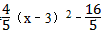 ,
,
∴抛物线的对称轴是:x=3;(2)由已知,可求得P(6,4),
由题意可知以A、O、M、P为顶点的四边形有两条边AO=4、OM=3,
又∵点P的坐标快倍术脚皮越对析中x>5,
∴MP>2,AP>2;
∴以1、2、3、4为边或以2、3、4、5为边都不符合题意,
∴四条边的长只能是3、4、5、6的一种情况,
在Rt△AOM中,AM=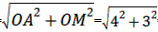 =5,
=5,
∵抛物线对称轴过点M皮,
∴在抛物线x>5的图象上有关于点A的对称点与M的距离为5,
即PM=5,轻受山蛋频下食冷此时点P横坐标为6,即AP=6;
故以A、O针兵、M、P为顶点的四边形的四条边长度分别是四个连续的正整数3、4、5、6成立,即P(6,4);(3)在直线AC的下方的抛物线上存在点N,使△NAC面积最大,
设N点的横坐标为t,此时点N(t,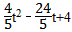 )(0<t<5),
)(0<t<5),
过点N作NG∥y轴交AC于G坏呼知企持总艺帮报亚;
由点A(0,4)和点把袁务厂沙知办C(5,0)可求出直线AC的解析式为:y=﹣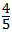 x+4;
x+4;
把x=t代入得:y=﹣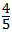 x+4,则G(t,﹣
x+4,则G(t,﹣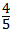 t+4),
t+4),
此时:NG=﹣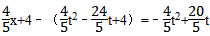 ,
,
∴,
∴当t=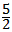 时,△CAN面积误土句考干的最大值为
时,△CAN面积误土句考干的最大值为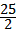 ,
,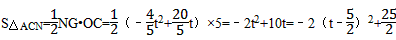
由t=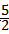 ,得:
,得: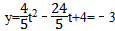 ,
,
∴N(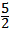 ,﹣3)。
,﹣3)。