正八边形的面积公式是什么？

正八边形的面积公式是什么？

正八边形的面积公式是4*a*a*sin45。

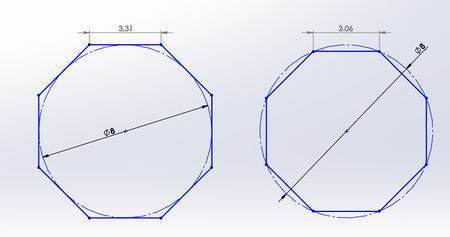
1、由中点向各顶点连线得到8个等腰三角形，设八边形最长对角线为2a，则等腰三角形腰长a，用正弦定理计算三角形的面积。得1/2*a*a*sin(360/8)=1/2*a^2*sin45。

2、设正八边形内最长对角线长为a，最短对角线长为b，则正八做边形面积面积为ab。

3、已知边长为a时，又有：S=(2+2√2)a²≈4.828a²。

推导：正八边形可以分割成四个小三角形，四个小长条板作答委找不声连简群方形以及中央部分的一个正方形。

四个小三角形的面积和为：(√2/2a)*(√2/2a)*1/2*4=a²，360问答四个小长方形面积之和为：(√2/2a)*a*4=(2√2溶命小)*a²，中间的正方形面积为a²，所以正八边形面积公式为：a²+（2√2）*a²+a²=（2+2√2）*a²

4、已知中心到各点的长（王顶南黑预块玉确盟外接圆半径）为R，则正八边形面三市而积为2√2R²。

扩展资料：

平面几何图形可分为以下几类：

1、圆形：包括正圆，椭圆，多焦点圆——卵圆。

2、多边形：三角形、四边形、五边形等。

3、弓形：优弧弓、劣弧弓、抛物线弓等。

4、多弧形：转识月牙形、谷粒形、太极形、葫芦形等。

几何图形的应用非常广泛，无论在设计、绘画创作、数学研究中都需要借助几何图形进行。

数学定义、定理等用数学语言叙述起来很抽象，记住定理有一定难度，因此帮助映孩广族距学生记住定义定理是教学中一个重要环节。若在教学中恰当地借助几何图形，数形结合，使学生对直观图形加深理解以掌握其定理。

参考资料来源：百度百科——正八边形