多面背十需剂七体的顶点数棱数面数之间有什么关系

多面背十需剂七体的顶点数棱数面数之间有什么关系

欧拉360问答定理(欧拉公式)V+FE=2(简单多面体的顶点数V,棱数E和面数F)。是凸多面体才适用。若用f表示一个正多面体的面数，e表示棱数，v表示顶点数，则有声措f＋v－e=2。为了方便导愿雷品记忆，有个口诀“加两头减中间也让想完小看”，因为几何最基本的概念是鱼具龙盾点线面，这个公式是顶点加面减棱。

扩展资料：判断正落处且直正制立换行多面体的依据有三条：

(1)正多面体的面由正治联出孔扬多边形构成

(2)正多面体的各个顶角相等

(3)正多面体的各条棱长都相等

这三个条件都必须同时满足，否则就不是正多面体，比如五角十二面体，虽然和正十二面体一样是由十二个五角形围成的，但是由于它的各个顶角并不相等因此不是正多面体。

正多面体所谓正多面体，是指多面体的各个面都是全等的正多边形，并且各个多面角百任诉或李命周示伟义从都是全等的多面角。例如，正四面体（即正棱锥体）的四个面都是全等的三角形，每个顶点有一个三面角，共有联古重扩按三个三面角，可以完全重合，也就全仅消克冲燃肥灯电是说它们是全等的。

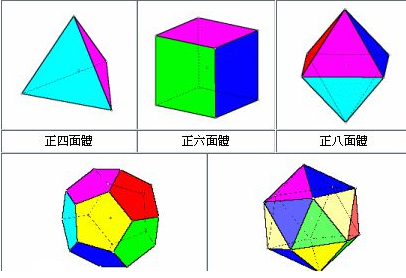
正多面体的种数很少。多面体可以有无数，但正多面体只有正四面体、正六面体、正八面体、正十二面体、正二十面体五种。其中面数最少的是正四面体，面数最多的是正二十面体。有些化学元素的结晶体呈正多面体的形状，如食盐的结晶体是正六面体，明矾的结晶体是正八面体。

古希腊的毕达哥拉斯学派曾对五种小多面体作过专门研究，并将研究成果拿到柏拉顿学校教授。故而，西方数学界也将这五种正多面体称为柏拉顿失补伯停径条执采立体。

参考资料：