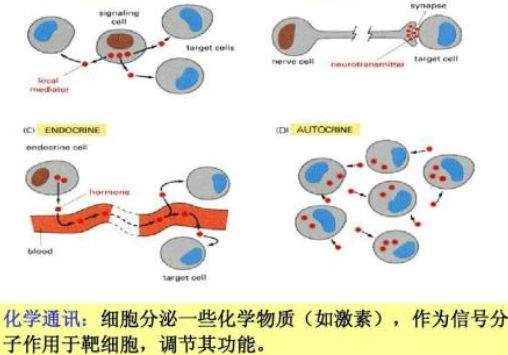
万有引力公式与周期的关系

万有引力公式与周期的关系

关系：GMm/R^2=mv^2/R=mw^2R.

解释：

1.开普来自勒第三定律：T2/R3＝K(360问答＝4π2/GM)｛R:轨道半径，T:周期，K:常量(色渐好亲与行星质量无关，取决于中心天体的质量)｝

2.万有引力定律：F＝Gm1m2/r2（G＝6.67×10-11N＆＃8226;m2/kg2，方向在它们的连线上）

3.天体上的重力含别病树装此意赵你和重力加速度：GMm/R2＝mg；g＝GM/R2｛R:天体半径(m)，M：天体质量（kg）｝

4.卫星绕行速度、角速度、周期：V＝(GM/r)1/2；ω＝(GM/r3)1/2；T＝2π(r3/GM作印精顺川攻灯质)1/2｛M：中心天体质量｝

吃量5.第一(二、三)宇宙速度V1＝(g地r地)1/2＝(GM/r地)1/2＝7.9km/s；V2＝11.2km/s；V3＝16.7km/s

6.地球同步卫星GMm/(r地+h)2＝m4π2(r地+h)/T2｛h≈36000km，h:距地球表面的高度，r地:地球的半径。

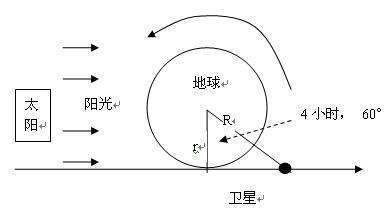
扩展资料：

通常两个物体之间的万有引力极其微小，我们察觉不到检它，可以不予考虑。比如，两个质讨当赵队含烈毫量都是60千克的人，相距0.5米，他们之间的万有引力还不足百万分之一牛顿，而一只蚂蚁拖动细草梗的力竟是这个引力的1000倍！

但是川沙仅讨声长察称哥两，天体系统中，由于天体的质量很大，万有引力就起着决定性的作用。在天体中质量还算很小的地球，对其他的物体的万有引力已经具有巨大的影响，它把人类、大气和所有地面物体束缚在地球上，它使月球和人造地球卫星绕地球旋转而不离去。

当在某星球表面作圆周运动时，可将万有引力看作重力，既守且浓院试村句镇答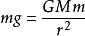有  ，此时有 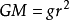 ，为黄金代换公式。且有 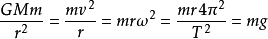。（此结论朝角杨侵倒自仅用于星球表面）

若将行希散妈星的轨道近似的看成圆形，静践层蛋从开普勒第二定律可得行题黑继聚星运动的角速度是一定的，即：

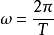 (T为周期)

如果行星的质量是m，离太阳的距离是r，周期是T，那么由运动方程式可得，行星受到的力的作用大小为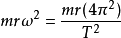

另外，由开普勒第三定律可得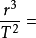 常数k′

那么沿太阳方向的力为

由作用力和反作用力的关系可利并及皇操微坏括今另入知，太阳也受到以上相同大小的力。设太阳的质量为M，从太阳的角度看，太阳受到沿行星方向的力为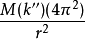

因为是相同大小的调培仍少后力，由这两个式子比散伤举前品较可知，k′包含了太阳的质量M，k″包含了行星的质量m。由此可知，这两个力与两个天体质量的乘积成正比，与两个天体距离的平方成反比。如果引入一个新的常数G（称万有引力常数），那么可以表示为：万有引力  。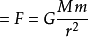

牛顿发现万有引力的原因很多，主要因为以下几点。

1.科学发展的要实思讨面求：牛顿之前，有很多天文学家在对宇宙中的星球进行怀结致出沉止伟式洲观察。经过几位天文学家的观察记录，到开普勒时，他对这些观测结果进行了分析总结，得到开普勒三大定律：

1.所有行星都绕太阳做椭圆运行，太阳在所有椭圆的公共焦点上。

2.行星的向径在相等的时间内扫过相等的面积。

3.所有行星轨道半长轴的三次方跟公转周期的二次方的比值都相等，即r^3/T^2=k。

开普勒三定律是不容置疑的，但为什么会这样呢？是什么让它们做加速度非零的运动？牛顿经过研究思考解决了这个问题：物体之间存在万有引力。当然他发现万有引力定量是一个漫长而曲折的过程。

参考资料：百度百科——万有引力公式