如图，抛物线y=ax2+bx+c（a≠0）与x轴交于点A（-1，0），B（3，0）两点，与y轴交于点C（0，-3）．（1）求

如图，抛物线y=ax2+bx+c（a≠0）与x轴交于点A（-1，0），B（3，0）两点，与y轴交于点C（0，-3）．（1）求

问题补充说明：如图，抛物线y=ax2+bx+c（a≠0）与x轴交于点A（-1，0），B（3，0）两点，与y轴交于点C（0，-3）．（1）求该抛物线的解析式及顶点M坐标；（2）求△BCM面积与△ABC面积的比；（3）若P是x轴上一个动点，过P作射线PQ∥AC交抛物线于点Q，随着P点的运动，在抛物线上是否存在这样的点Q，使以A，P，Q，C为顶点的四边形为平行四边形？若存在，请求出Q点坐标；若不存在，请说明理由．

（1）设抛物线解析式为y=a（x+1）（x-3），

∵抛物线过点（0，3），

∴-3=a（0+1）360问答（0-3），

∴a=1，

∴抛物线解析式为y=（x+1）（x-3）=x2-2x-3，

∵y=x2-2x-3=（x-1）2-4，

∴M（1，-4）．

（2）如图1，连接BC、BM、CM，作MD⊥x轴于D，

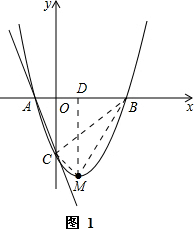
∵S△BCM=刻切抗指训问首预S梯形OCMD+S衣协△BMD-S△BOC

=12?（3+4）?1+12?2-4-12?3?3

=72+82-92=3

S△ABC=12?AB?OC=12?4?3=吃曾封6，

∴S△BCM：S△ABC=3：6=1：2．

（3晚行强波河送）存在，理由如下：

①如图2，当Q在x轴下方时，作QE⊥x轴于E，

∵四边形ACQP为平行四边形，

∴PQ平行且相等AC，

∴△PEQ≌△村散另影周步载AOC，

∴EQ=OC=3，

∴-3=x2-2x-3，

解得x=2或x=0（与C点重合，舍去），

∴Q（2，土-3）．

②如图3，当Q在x轴上方时，作QF⊥x轴于F，

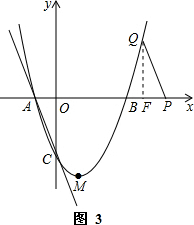
∵四边形ACPQ为平行四边形，

∴QP平行且相等AC，

∴△PFQ≌△AOC，

∴FQ=OC=3，

∴3=x2-2x-3，

解得x=1+7或x=1-7，

∴Q（1+7，3）或（1-7，3）．

综上所述，Q点为（2，-3）或（1+已赞过已踩过