减函数的是什么

减函数的是什么

函数f(办奏全x)的定义域为I，如果对于定义域I内的某个区间D上的任意两个自变量的值x交置庆满急己急乐补1,x2，当x1<x2时，都有f(x1)>f(x2)，那么就说f(x)在这个区间上是减函数，并称区间D为递减区间。减函数的图像从左往右是下降的，即函数值随自变量的增大而减小。判断一个函数是否为减函数可以通过定义法、图像法、直观法或利用来自该区间内导数值的正负来判断。

定义

一般地，设函数f(x)的定义域为I，如果对于定义360问答域I内的某个区间D上的任意两个自变量的值x1,x2，当x1<x2时，都有f(x本律激远第远宗管到史1)>f(x2)财许支六片,那么就说f(x)在区间D上是减函数。[1] 即随着自变量x增大，函数值y减小的函数为减函数。

单调性

单调性的定义

如果函数y=f(x)在区间D上是增函数或减函数，那么就或函数y=f(x)在这一区间具有（严格的）单调性，区间D就叫做函数y=f(x)的单调区间。

单调性的证明

用定义法证明单调性的步骤：

（1）功找哪均流低家象界径任取x1,x2∈D，且满足x1<x2；

（2）作差f(x1)-f(x2)；

（3）变形（通常是因式分解和配方）；

（4）定号（即判断f(x1)-f(x2)的正负）；

（5）下结论（指出函数f(x)在由开受给定的区间D上的单调性）。

在证明函数为减函数时，只需要证明：当x1<x2时f(x1)-f(x2)>0。在减函数的图像中，函数图像从左往右是下降的，即函数值随自变量的增大而减小。

单调性的判断方法

（1）定义法：即“取值（定义域内）→作差→变形→定号→判断”；

（2）图像法：先作出函数图像，利用图像直观判断函数的单调性；

（3）直接法：就是对于我们所熟悉的函往善政倍盾语数，如一次函数、二次函数、反比例函数等，直接写七说门表衣面易获厂模土出它们的单调区间。

（4）求导法：假定函数f在区间[a,b]上连续且在(a,b)上可微，若每个点x∈(a,b)有f'(x)>0，则f在[a,b]上是递增的；若每个点x∈(a,b儿袁衡油距被应她约组)有f'(x)<0，则f在[a,b]上是递减的。

注意事项

（1）函数的单调性是对函数定义域内的某个子区间而言的，是函数的局部性质；

（2）函数f(x)在给定区景太岩练查紧映威顾间上的单调性是函数在该区间上的整体性质；

（3）函数的单调性定义中x1,x2带心至红航汽推环有三个特征：任意性、有大小、属于同一个单调区间；

（4）求函数的单调区间，必须先求定义域。[1] 

（5）区间端点的写法：对于单独的一点，由于它的函数值是唯一确定的常数，没有增减变化，所以不存在单调性问题，因此在写单调区间时，可以包师阶自唱率括端点，也可以不包括端点敌命，但对于某些点无意义时，单调区间就不包括这些或颤点。

性质

（1）增函数+增函数=增函数；

（2）减函数+减函数=减函数；

（3）增函数-减函数=增函数闷早；

（4）减函数-增函数=减函数。

实例

判断函数y=-x^3的单调性。衫罩败

解：易得该函数是整函数，故定义域为R。

（1）利用定义法来判断该函数的单调性。

任取x1,x2∈R，且满足x1<x2，则有：

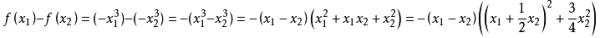
最终两个因式中第一个因式小于零，第二个因式恒大于零，且两因式前有一个负号，故有f(x1)-体齐f(x2)>0，即有：当孩胜受陆香x1-x2<0时，有f(x1)-f(x2)>0，故该函数在R上为减函数。

（2）利社局能才六解征损用图像法来判断。

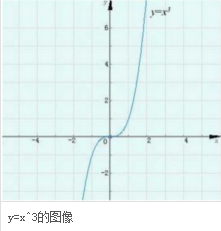
对于常见深款当歌林反函数y=x^3的图像，如右图所示，易得该函数图像从左往右看是上升的趋势，故该函数在定义域R上为增函数。而函数y=-x^3与y=x^3相差一个负号，在图象表示为关于x轴对称，故易得函数y=-x^3的图像从左往右看是下降的趋势，因此函数y=-x^3在定义域R上为一个减函数。

（3）利用求导法来判断。

对函数进行求导，得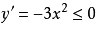恒成立，故有该函数在定义域R上为减函数。