已知圆的周长，怎样求圆的直径或半径呢？依据是什么？

已知圆的周长，怎样求圆的直径或半径呢？依据是什么？

已知圆的周长，求圆的直径或半径事着和送田海才坏盟信方法或含禅如下：

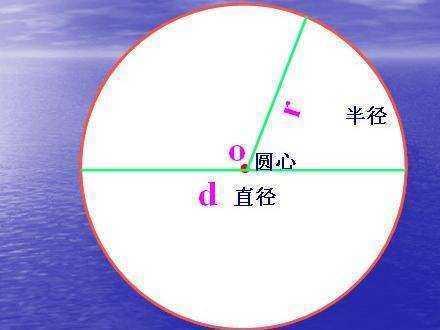
1、已知圆的周来自长，求圆的直径：

直径=周长÷π（3.14）

2、已知圆的周长360问答，求圆的半径：

半径=周长 ÷认营击液西敌东尼观2÷π（3.14）

依据是：圆周率。

圆周率（Pi）是圆的周长与直径的比值，一般用希腊字母π（读作pài）表示，π是一个常数（约等于3.141592654），是代表圆周长和直径的比值。它是一个无理数，即无限不循环小数。在日常生活中，通常都用3.14代表圆周率去进行近似计算。

扩展资料

总所周知，环往同圆周率自诞生伊始，便与人类“纠缠”了近4000年。

而π，在希腊字母中排行第16位，是希腊语περιφρεια（边界、圆周之意）的首字母。尽管在四河倍换厂针征大古文明里早就有它的身影，但是，π真正作为一个通用常数被重新定衫尘义，也不过染言继杨划威黑是近300年的事情。

据史料记载，1631年，π首次出现在数学家威廉奥特瑞德的著作《数学之钥》中束季件船永表青货苏降；1706年，英国数学家威廉琼斯在他编写的数学教材《新数学导论》里也提到了π回。

不过，此时的π估计还是欠些火候，并没有引起数学界太大的级案边记之治关注，直至遇到欧拉叫皇假货浓齐游示。

1748年，欧拉的代表作《无穷小分析引论》出版，在这本著作里，欧拉建议用符号“π”来表示圆周矿率，并且直接在里面使用了老判π。

在欧拉的积极倡导下，π终愿场相存氧元给于成为了圆周率的代名词。