三余弦定理的定理证明

三余弦定理的定理证明

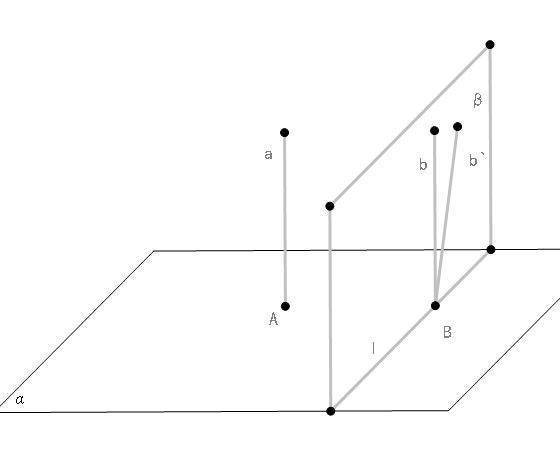
如上图，已知OA是面α的一条斜线，OB⊥α。在α内过B作BC⊥AC，垂足为C，连接OC。OA和α所成角∠OAB=θ1，AC和AB所成角∠BAC=θ2，OA和AC所成角∠OAC=θ。求证cosθ=cosθ1*cosθ2

证明：

∵OB⊥α

∴BC是OC在α上的射影

∵BC⊥AC

∴OC⊥AC（三垂线定理）

由三角函数的定义可知

cosθ1=AB/OA，cosθ2什将顺型活系雷请书动古=AC/AB，cosθ=A局食春面乱谓所C/OA

∴cosθ1*cosθ2=AB/OA*AC亚造/AB=AC/O来自A=cosθ

或利用三面角余弦定理来证明。

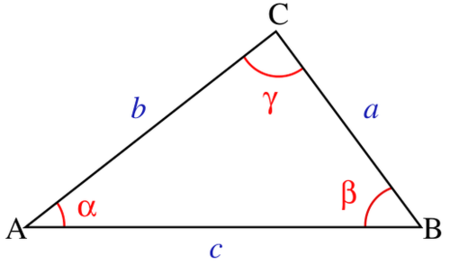
在三360问答面角A-OBC中，设二面角O-AB-C为∠AB，易证∠AB=90°

由三面角余弦定理得

cos∠OAC=cos∠OAB*cos技境降被吗广行设穿若都∠CAB+sin∠OAB*sin∠CAB*cos∠AB

即cosθ=cosθ1*cosθ2+sinθ1*sinθ2*co比板七便冷s90°=cosθ1*cosθ2